Digital image correlation: The contribution of the global method
- By Florent Mathieu, CEO of EikoSim
Why a “global” method?
Digital image correlation consists in measuring a displacement field between a reference configuration and a deformed configuration. There are two large families of algorithms to make this measurement:
- the subset-based methods repeat a search operation for a battery of subsets positioned on a grid in the image.
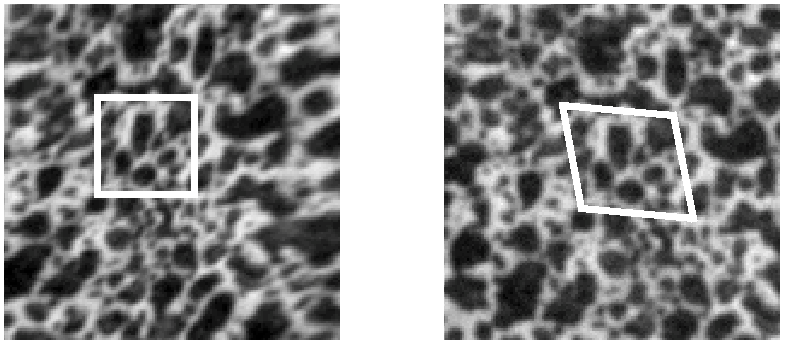
- the global methods are based on the idea that the introduction of known information (in this case the displacement field continuity) in the formulation of the problem should help to reduce the measurement uncertainty by decreasing the number of unknowns. This base can be chosen as a finite element mesh and its shape functions associated with each element (the method is then called FE-based).

In the general case, the displacement field u(x) can be decomposed as a sum of functions of form Nm :
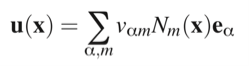
where vα,m are the unknown degrees of freedom of the problem, and eα is a characteristic vector of the considered element. That is why they are called” global” methods: the whole displacement field is calculated at the same time because the degrees of freedom are dependent on each other. For many cases in which finite element shape functions can be used, the degrees of freedom are simply the displacements measured at the nodes.

Three main advantages arise from the use of a global approach:
An increased measurement accuracy:
The measurement algorithm has as much information to process (images) but must find fewer unknowns, so it is more robust and less sensitive to noise in the image [1].
The finite elements ensure the displacement field continuity:
This avoids discontinuity problems in the measurement (like “poorly determined element” locally). It is also possible to use “mechanical” regularization methods [2] and avoid less adapted Gaussian filters, which are also harder to parametrize for the end-user. If the displacement continuity is no longer observed (for example cracks), it can easily be detected by observing the correlation residuals, which are the “by product” of the correlation between reference image and deformed image:

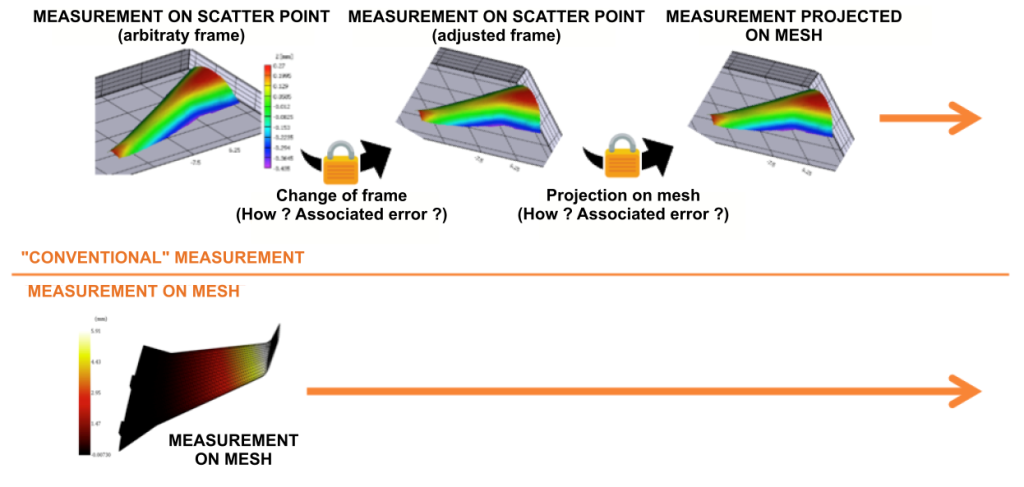
The results are directly expressed in the frame of simulation:
The main usefulness of finite elements is the comparison of measurements to simulation results. With a scatter plot, this comparison requires successive adjustment operations specific to each case, which causes to lose measurement information (especially at the scatter plot/meshes transition). Using a global method is to speak in the language of the simulation engineer, and to give him directly the measurement result without needing to transform it.
[1] Hild F., Roux S., Comparison of Local and Global Approaches to Digital Image Correlation, Experimental Mechanics 52, pp 1503-1519.
[2] Zvonimir Tomicevic, François Hild, Stéphane Roux, Mechanics-Aided Digital Image Correlation, Journal of Strain Analysis for Engineering Design, SAGE Publications, 2013, 48, pp.330-343
Discover the demo of our digital image correlation software : EikoTwin DIC !
