Les sources d’erreurs de mesure par corrélation d’images numériques

• Par Clara Minguet, Ingénieure de recherche, chez EikoSim

En corrélation d’images numériques comme dans tout processus de mesure, des erreurs viennent affecter les données mesurées. La particularité de cette méthode réside dans la dépendance directe entre l’essai et l’erreur de mesure [1,2,3]. En effet, elle doit être caractérisée pour chaque nouvel essai. Ces erreurs peuvent être classées en deux catégories : le biais correspondant aux erreurs systématiques et l’incertitude correspondant aux erreurs aléatoires. Pour plus de détails sur le biais, l’incertitude et la façon de les quantifier, je vous invite à lire l’article dédié sur notre blog. Dans cet article, on présentera les différentes sources de ces erreurs (biais et incertitude) qui peuvent affecter les mesures par corrélation d’images numériques. Ces sources pourront être distinguées en deux types : les sources d’erreurs propres à l’essai et au post-traitement qu’il convient de mitiger afin de fiabiliser les mesures de déplacements et celles inhérentes au code de corrélation d’images numériques utilisé, souvent non modulables par l’utilisateur. Ce deuxième type de sources d’erreurs de mesure ne sera pas développé dans la suite car il fera le sujet d’un prochain article de blog.

Sources d’erreurs liées à l’essai

Parmi les sources d’erreurs intervenant lors de l’essai instrumenté par corrélation d’images numériques, il y a des sources propres au matériel d’essai et plus précisément aux caméras utilisées, des sources propres à l’environnement d’essai et des sources propres au mouchetis.

Sources d’erreurs propres au matériel d’essai : bruit stationnaire des capteurs des caméras

Ce bruit numérique de la caméra correspond à une variation temporelle du niveau de gris de chaque pixel autour de sa valeur « vraie » indépendamment de ses voisins et du pas de temps. Son modèle de bruit associé est toujours blanc gaussien ou poissonnien. Cet effet, dépendant de la qualité du capteur, induit une dégradation de la qualité du signal. En effet, pour des capteurs de mauvaise qualité, l’image devient même « granuleuse » à l’œil nu (voir Figure 1). L’impact final sur la mesure de déplacements est de l’ordre du centième de pixel pour un capteur CMOS/CCD standard en bon état. Il existe plusieurs sources de bruit numérique. Les 3 principales sont le bruit de photons dû à la variation temporelle du flux de photons, le bruit de lecture qui est une incertitude sur la mesure du courant électrique dépendant du gain du capteur et le bruit thermique dû à l’élévation de la température de la caméra.

L’équivalent du bruit numérique pour une caméra IR est le NETD (Noise Equivalent Temperature Difference), de l’ordre de quelques mK. C’est la plus petite différence de température détectable.

Sources d’erreurs propres à l’environnement d’essai

• Qualité de l’éclairage

Un éclairage insuffisant et des variations de brillance/contraste spatiales et temporelles [4] multiplient par 10 le niveau d’incertitude « classique » engendrant ainsi une incertitude sur les déplacements mesurés de l’ordre du dixième de pixel. Pour le deuxième point, il convient donc de régler son éclairage de tel sorte qu’il soit homogène et constant tout au long de l’essai. Pour cela, il faut analyser en amont les conditions d’éclairage du lieu d’essai et tenter de les maîtriser au mieux, ce qui n’est pas toujours évident notamment dans des lieux bénéficiant d’un fort éclairage naturel.

• Effets convectifs

Des mouvements convectifs de l’air environnant, appelés brumes de chaleur, peuvent apparaître lors d’un essai instrumenté par corrélation d’images numériques [5]. Ce phénomène entraîne une distorsion apparente des images et parasite donc les mesures de déplacements. Il est bien sûr courant lors d’un essai à hautes températures. Cependant, il peut intervenir également lors d’un essai long réalisé à température ambiante sous l’effet de l’échauffement de l’air par le dispositif d’éclairage, ou par le seul effet de la machine d’essai. Il va de soi que l’amplitude du déplacement parasite n’est pas équivalente dans les deux cas. En effet, pour un essai à température ambiante, on observe des amplitudes de l’ordre de 0,1 à 0,5 px alors que pour un essai à hautes températures supérieures à 600°C, l’amplitude peut atteindre plusieurs pixels. Quoi qu’il en soit, les mouvements convectifs ont un fort impact sur l’incertitude de mesure. Pour un essai à température ambiante, ils multiplient par 20 le niveau d’incertitude « classique » engendrant ainsi une incertitude sur les déplacements mesurés de l’ordre de 0,2 px. Une des solutions expérimentales souvent retenue pour atténuer les effets convectifs est l’utilisation d’un ventilateur entre les caméras et la pièce testée, pour créer un flux d’air laminaire.

• Biais externes

Lors d’un essai instrumenté par corrélation d’images numériques, des biais externes peuvent intervenir. Deux types de biais externes peuvent être rencontrés : les biais permanents comme les vibrations transmises depuis le sol ou inattendus comme un mouvement des caméras ou d’un panneau LED au cours de l’essai. Le balisage de la zone d’essai est déjà une première action à mettre en œuvre afin de limiter certains biais externes inattendus pouvant être provoqués par une inattention des personnes présentes lors de l’essai.

Sources d’erreurs propres au mouchetis

• Qualité du mouchetis

Le mouchetis est un élément clef en corrélation d’images numériques. Il se doit d’être mat afin d’éviter les reflets à la surface de la pièce d’intérêt. De plus, un bon mouchetis a une distribution de taches aléatoire et présente un niveau de contraste élevé entre les taches sombres et claires. En résumé, l’histogramme des niveaux de gris associé doit être étalé avec une répartition équivalente de blanc et de noir.

• Rapport entre la taille des taches de mouchetis et la taille des pixels

En plus du contraste, du rendu mat et du caractère aléatoire du mouchetis, il est indispensable que la taille de la texture soit assez grande par rapport à la taille physique d’un pixel pour éviter ou au moins réduire les erreurs associées. En effet, il faut qu’il y ait suffisamment de pixels par tache de mouchetis dans les images. On conseille une taille minimum de tache de 4 pixels de diamètre.

• Rapport entre la taille des taches de mouchetis et la taille des éléments

Une autre règle vient contraindre la taille des taches de mouchetis. Effectivement, il faut qu’il y ait suffisamment de contraste par imagette soit en d’autres termes, suffisamment de taches de mouchetis par élément dans le cadre de la méthode globale FE-based (voir Figure 2) ou par subsets dans le cadre de la méthode locale. On recommande que chaque imagette contienne au moins 4 taches.

Afin de réduire au maximum les erreurs dues à la taille du mouchetis, n’hésitez pas à vous servir de la feuille de calcul mise à disposition sur notre site.

Sources d’erreurs liées au post-traitement

Les erreurs intervenant lors du post-traitement des images d’essai proviennent de la sélection des points de pré-étalonnage par l’utilisateur et de l’utilisation de stratégies régularisantes.

• Sélection des points de pré-étalonnage (spécifique à EikoTwin DIC)

Dans le logiciel EikoTwin DIC, afin d’initialiser l’algorithme d’étalonnage des caméras, l’utilisateur doit positionner manuellement des points de pré-étalonnage au même endroit sur l’image de référence et sur le maillage par éléments finis. Le choix de ces points varie nécessairement d’un utilisateur à un autre. Cependant, l’erreur résultante peut facilement être limitée en cliquant minutieusement les points et en respectant certains critères.

• Application de stratégies régularisantes (filtrage, régularisation mécanique)

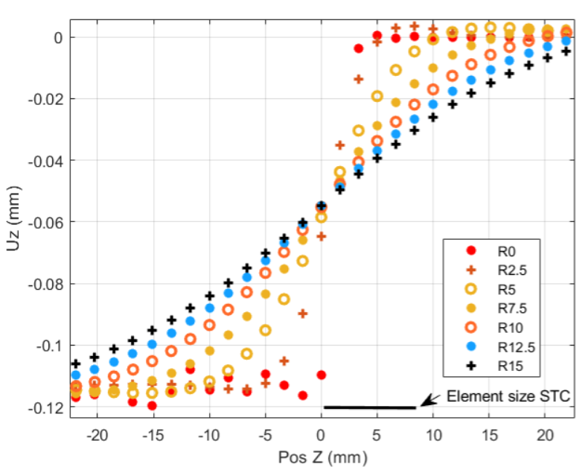
Ces deux techniques permettent de réduire les fluctuations spatiales parasites du champ de déplacements mesuré avec un logiciel de corrélation d’images numériques. Le filtrage et la régularisation mécanique peuvent être vus comme des filtres passe-bas, le premier s’appliquant au champ de mesure solution et le deuxième directement dans l’algorithme par intégration des hypothèses de compatibilité des champs de déformation avec les équations mécaniques. Dans les deux cas, le choix par l’utilisateur d’un filtrage trop sévère ou d’une longueur de régularisation trop élevée par rapport au gradient de déformation expérimental entraîne un lissage trop important des données. Ce choix doit donc être fait avec rigueur car il est source de biais sur la quantité mesurée [3] (voir Figure 3).

L’un des avantages de la régularisation mécanique par rapport à un lissage générique est le lien direct entre la longueur de régularisation pertinente et la physique du phénomène observé. En comparant cette longueur à un résultat de simulation pour l’essai considéré, l’utilisateur va immédiatement voir si la longueur retenue est pertinente par rapport au gradient de déformation attendu. On peut également souligner qu’un champ régularisé par cette technique est mécaniquement admissible, contrairement au cas d’un filtrage gaussien par exemple.

Vers une meilleure intégration des erreurs de mesure …

Pour résumé, les sources d’incertitudes et de biais sur la mesure par corrélation d’images numériques sont très variées. Cependant, la plupart de ces erreurs peuvent être limitées par une préparation et une instrumentation rigoureuse de l’essai. Afin de valider la mesure, il est important de quantifier le bruit de fond d’un essai de façon à s’assurer que les données mesurées à un instant donné correspondent bien à du signal et non du bruit. Contrairement au biais, il existe un moyen efficace de déterminer l’incertitude de mesure a posteriori à partir d’images prises au repos lors de l’essai. A cette fin, un module de calcul de l’incertitude sera disponible fin 2021 dans le logiciel EikoTwin DIC. De plus, grâce à une pré-étude avec le logiciel EikoTwin Virtual, il est maintenant possible d’estimer une borne inférieure de l’incertitude avant l’essai. En effet, lors de la pré-étude, la plupart des sources d’erreurs listées dans cet article sont simulées au plus proche de la réalité. Ce travail en amont permet ainsi à l’utilisateur de valider son essai ou de le modifier en conséquence.

De manière générale, nous vous recommandons pour continuer vos lectures de télécharger le guide des bonnes pratiques en corrélation d’images numériques [3], désormais disponible en français !

---

Références

[1] André Chrysochoos, Yves Surrel. Basic elements of metrology and introduction to the various techniques in: Full-Field Measurements and Identification in Solid Mechanics, Michel Grediac (Editor), Francois Hild (Editor). Wiley-ISTE, 2012, 978-1-118-57847-6.

[2] Reu, Phillip L., Miller, Timothy J., Sutton, Michael, and Wang, Yanqing. Uncertainty quantification for digital image correlation. United States: N. p., 2009. Web.

[3] iDICs, A Good Practices Guide for Digital Image Correlation: Standardization, Good Practices, and Uncertainty Quanti­cation Committee, October 2018.

[4] F. Hild and S. Roux, Digital Image Correlation in: Optical Methods for Solid Mechanics:A Full-Field Approach. P. Rastogi and E. Hack, eds., Wiley-VCH, Weinheim (Germany, 2012), pp. 183-228.

[5] Jones, E., Reu, P. Distortion of Digital Image Correlation (DIC) Displacements and Strains from Heat Waves. Exp. Mech., 58, 1133–1156 (2018).