Comment réaliser un mouchetis adapté à la Corrélation d’Images Numériques ?

• Par Floriane Soulas, Ingénieure R&D chez EikoSim

Contexte

Le principe de la corrélation d’images numériques est basé sur le suivi d’informations d’une image dite « de référence » dans les images suivantes, souvent appelées « images déformées ». L’ensemble des images forme un film, dont on cherche à extraire une mesure.

On peut donc voir la corrélation d’images comme du suivi de points sur toute la surface observée : suivre les déplacements d’une surface d’une pièce est équivalent à suivre les déplacements de tous les points de cette surface. Cela nécessite que la pièce soit « texturée » : s’il n’y a qu’un point noir, on ne peut pas mesurer le déplacement et la déformation de la zone blanche qui l’entoure. Pour qu’un point soit reconnu, il faut une texture aléatoire qui permet de reconnaître la zone autour du point d’intérêt. Cette texture est appelée mouchetis.

La plupart du temps, les mouchetis sont réalisés à la bombe. On vient pulvériser des taches de peinture noir mat, de tailles aléatoires, sur un fond blanc, mat lui aussi afin d’éviter les reflets qui pourraient gêner la mesure. Un mouchetis de points blancs sur fond noir est aussi possible.

Afin d’atteindre des tailles de taches de l’ordre de la dizaine de microns, il est possible d’utiliser un aérographe, comme expliqué dans l’article sur la corrélation d’images pour les structures treillis.

Qu’est ce qu’un bon mouchetis ?

Pour réaliser un bon mouchetis, celui-ci doit être :

• Aléatoire
• Avec des tailles de taches adaptées à la mesure réalisée.

Pour vérifier que le mouchetis est bien aléatoire et ne comporte ni trop de noir ni trop de blanc, on peut s’aider des histogrammes de niveaux de gris. Un histogramme optimal est un histogramme « plat » avec une répartition équivalente de blanc et de noir.

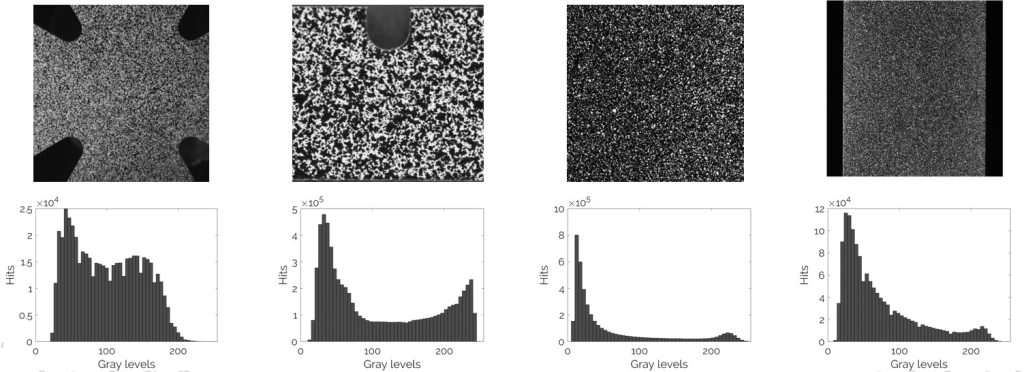
Il faut également veiller à adapter la taille des taches, cela résulte d’un compromis entre le phénomène étudié (taches fines) et la résolution de l’imageur (taille suffisamment large pour être visible par le capteur).

Réaliser un mouchetis à la bombe de peinture

Différents types de mouchetis « utilisés » lors des essais EikoSim

Il est parfois possible de se passer de l’étape du mouchetis. En effet, certains matériaux, comme le béton, ont même une texture « naturelle » qui présente une hétérogénéité suffisante pour agir comme un mouchetis naturel, ainsi que le montre la Fig. 4. Avec ce type de surface, il est possible de traiter directement les images sans venir peindre la structure.

Pour les cas où l’on souhaite étudier des déplacements de corps rigide, sans déformation, il est possible de créer numériquement un mouchetis et de l’imprimer sur des feuilles autocollantes, que l’on viendra déposer sur la structure à étudier. L’avantage de cette technique réside en ce que le caractère aléatoire ainsi que la gestion de la taille des taches sont entièrement contrôlés par l’utilisateur qui peut choisir lui-même les diamètres min et max de ses taches de mouchetis.

Enfin, il existe encore d’autres méthodes, comme celle mise au point par ALPhANOV

écrit et illustré dans cet article par Girolamo MINCUZZI et Simon NOURRY

Il est bien connu qu’après avoir irradié la surface d’un matériau comme un métal, un semi-conducteur ou même un diélectrique transparent avec quelques impulsions ultracourtes, il est possible de modifier la morphologie de la surface en générant des ondulations de sous-longueurs d’onde. Ces ondulations sont perpendiculaires à la direction de polarisation et sont appelées structures de surfaces périodiques induites par laser LIPSS (voir Fig.6 (a) et (b)). 

En augmentant le nombre N d’impulsions, le LIPSS tend à se transformer en micro-rainures parallèles à la direction de polarisation (voir Fig.6 (c) et (d)). Enfin, en augmentant encore le nombre d’impulsion, des pointes, de taille caractéristique de ≈10 µm, apparaissent à la surface (voir Fig.6 (e) et (f)).

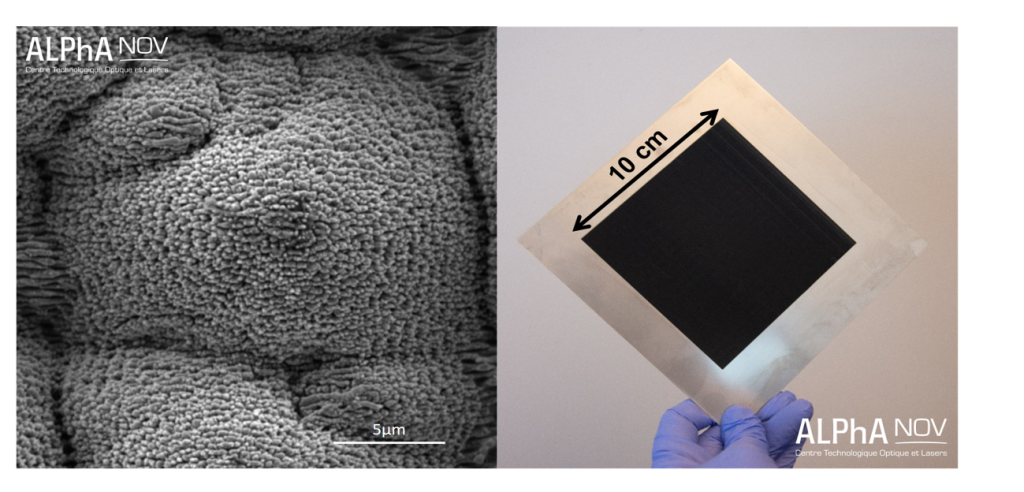
Grâce à ces structures de surface, il est possible de contrôler la réflectivité de surface R sur une large gamme de valeurs. Il est intéressant de noter que dans le cas de surfaces recouvertes de pointes, la lumière subit une réflexion multiple permettant un mécanisme de piégeage de la lumière réduisant R < 10%. Cet effet est renforcé lorsque la surface des pointes est constituée de pores nanométriques. Dans ce dernier cas (voir Fig.7 à gauche), des valeurs de R < 5% peuvent être obtenues, ce qui donne un effet de « noir profond » (voir Fig.7 à droite).

De plus, grâce à l’utilisation synchronisée des scanners à rayon laser et des translations, il est possible de traiter efficacement des surfaces plus grandes qu’un seul point d’impulsion et variant de quelques dizaines de microns à près d’un mètre.

Nous avons ici effectué une étude préliminaire et systématique de la façon dont les paramètres du processus, comme la vitesse de balayage, la trappe, le nombre de balayages successifs, l’énergie d’impulsion, auront une incidence sur la morphologie et la valeur R d’une surface en acier inoxydable de type miroir. Pour tous les essais, nous avons utilisé un laser pulsé de 350 fs émettant à λ = 1030 nm avec une fréquence de répétition de 500 kHz (Tangerine Amplitude Systèmes) et une taille de point 2ω0 ≈ de 35 µm. Les valeurs de R ≈ 20% correspondant à une couleur grise ont été trouvées pour des surfaces ayant une taille comprise entre 1cm² et 0,2mm × 0,2mm en utilisant le même ensemble de paramètres.

En revanche, pour R< 5%, nous avons observé que la taille de la surface traitée a une énorme influence sur le résultat final. Par exemple, la figure 8 (droite) montre le cas de deux morphologies de surface et de couleurs similaires (R<4%). Alors que la figure 8 (gauche) est relative à un 1cm² et a été traitée avec une énergie d’impulsion de E = 50 µJ, la figure 3 de droite est relative à 100µm × 200µm et a été traitée avec E = 32 µJ.

Enfin, nous avons utilisé tous les résultats obtenus lors de cette enquête préliminaire pour traiter une surface de 10cm × 10cm. Nous avons réalisé deux modèles différents ayant des caractéristiques de taille différente et variant de quelques cm2 à ≈100 µm×100 µm. Les résultats sont présentés dans la figure 9. 

Nous avons ainsi pu réaliser un mouchetis présentant différents niveaux de gris (en mélangeant la création aléatoire de blanc, de gris et de noir), sur une surface acier miroir. Ce mouchetis spécifique a ensuite été utilisé lors d’une étude par stéréo-corrélation en collaboration avec EikoSim.