Erreurs de mesure et corrélation d’images numériques

Par Pierre Baudoin, Ingénieur de recherche chez EikoSim

Lorsque l’on mène une campagne d’essais instrumentée par corrélation d’images numériques, il faut pouvoir déterminer l’erreur de mesure caractéristique pour les quantités d’intérêt étudiées (déplacement ou déformation mesurée). Ainsi, cela permet de déterminer si la mesure réalisée relève bien du « signal » recherché et non du « bruit » de mesure. Toute mesure doit être mise en rapport avec ce niveau d’incertitude, sinon on ne peut pas statuer sur sa pertinence. Une spécificité de la corrélation d’images numériques est que l’erreur de mesure doit être caractérisée à chaque nouvel essai. En effet, celle-ci dépend de nombreux paramètres qui varient d’un essai à l’autre (éclairage, mouchetis, caméras et objectifs utilisés…). Afin d’y voir plus clair, cet article propose de présenter les erreurs que l’on peut rencontrer sur un essai de corrélation d’images numériques. Il sera également vu comment il est possible les quantifier afin de valider un résultat de mesure.

Erreur aléatoire et erreur systématique

Les erreurs qui peuvent entacher une mesure peuvent être regroupées en deux grandes catégories (Figure 1). Ainsi, on parle des erreurs aléatoires (le « bruit » de mesure) et des erreurs systématiques (le biais).

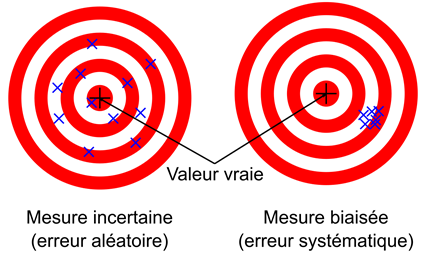
Pour une quantité d’intérêt donnée, l’erreur aléatoire (également appelée incertitude ou « bruit » de mesure) correspond à la dispersion des valeurs mesurées autour de la moyenne mesurée. La source principale d’erreur aléatoire en corrélation d’images numériques est le bruit de caméra. Ce sont les fluctuations temporel des niveaux de gris perçus par chaque pixel du capteur caméra observant un objet fixe.

D’autre part, l’erreur systématique (ou biais) correspond à un décalage de la valeur moyenne du signal mesuré avec la valeur moyenne du signal vrai. Parmi les sources de biais, on peut citer un mauvais étalonnage des caméras ou un mouvement de caméra intempestif intervenant en cours d’essai. De plus, dans le cas spécifique de la méthode globale, le choix d’une longueur de régularisation trop grande vis-à-vis du gradient de déformation expérimental peut aussi entraîner une mesure biaisée. Afin de limiter les sources d’erreurs citées, des articles sur l’étalonnage ou la régularisation figurent sur notre site.

Notons que s’il est toujours possible de quantifier l’erreur aléatoire (la dispersion de la mesure), il est en général impossible de quantifier le biais. En effet, il s’entend comme un écart avec une valeur vraie qui est inconnue. Ce n’est pas le cas pour certains cas particulier sur lesquels nous reviendrons dans la dernière partie de cet article.

Calcul d’incertitude

Le but de l’évaluation du « bruit de fond » est de déterminer l’amplitude de la dispersion de la valeur mesurée. Cette évaluation doit se faire dans les mêmes conditions que l’essai, par souci de répétabilité. Afin de caractériser cette dispersion, la méthode la plus simple est de prendre une série d’images sans mouvement de la pièce étudiée (sans effort ou déplacement imposé) dans les conditions d’essai puis de traiter cette série d’images à l’aide du logiciel de corrélation d’images numériques. Une mesure « parfaite » fournirait un champ de déplacement nul, pour toute la pièce et pour toutes les images traitées. La mesure étant cependant perturbée par le bruit, tout écart à zéro dans les champs mesurés correspond bien à une erreur de mesure.

Ensuite, il reste à caractériser l’amplitude de ce bruit, ce qui est couramment réalisé par le calcul de l’écart-type. Dans ce qui suit, on appellera U_i^j le déplacement mesuré au nœud i pour l’image j. Par souci de clarté, on omettra la composante considérée pour le calcul. Cependant, les calculs d’incertitudes présentés sont à réaliser et à analyser composante par composante. La démarche sera identique pour l’estimation de l’incertitude sur les composantes de la déformation. On commencera par calculer l’écart-type temporel nodal sur l’ensemble des nœuds du maillage de mesure. Celui-ci est donnée pour le nœud i par :

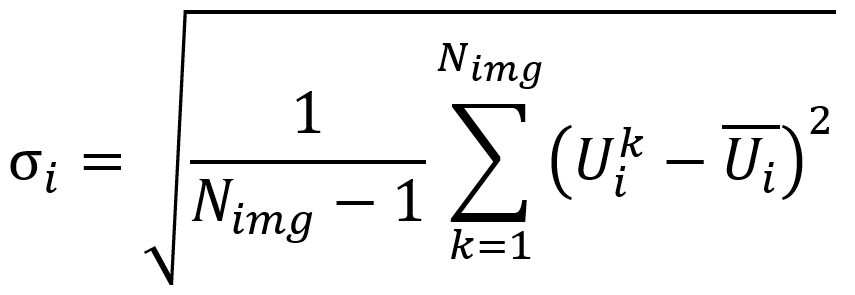
Où N_img est le nombre d’images statiques prises en compte pour le calcul de l’incertitude, et est la moyenne du déplacement mesuré au nœud i sur l’ensemble des images statiques. On en déduit l’incertitude temporelle U_t en prenant la moyenne de ces écarts types nodaux sur l’ensemble des N_noe  nœuds du maillage de mesure :

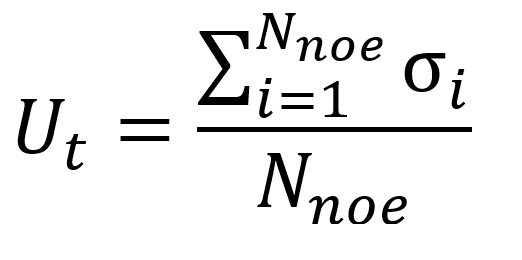
Une seconde métrique rencontrée pour ces calculs d’incertitudes est celle de l’incertitude spatiale. Pour ce faire, on commence par calculer l’écart-type du déplacement pour une image donnée. Cela nous permet d’évaluer la quantification de la dispersion du déplacement mesuré sur l’ensemble des nœuds du maillage de mesure. On moyenne ensuite cette quantité sur l’ensemble des images acquises.

Ces deux estimations fournissent généralement des valeurs semblables. On peut alors se baser sur ces valeurs pour déterminer si une quantité d’intérêt sera mesurable ou non pour un dispositif expérimental donné. En général, on considère que la mesure réalisée correspond bien à du signal si son amplitude est supérieure à 3 fois cette incertitude, sinon, la mesure n’est pas distinguable du bruit de mesure.

Recommandations pratiques :

• Acquérir au minimum une dizaine d’images statiques dans les conditions d’essai (caméras, objectifs, éclairement, température, mise en route éventuelle des machines d’essai environnantes, etc.).
• Le traitement des images doit être réalisé dans les mêmes conditions que l’essai lui-même. On utilise alors le même maillage de mesure, même critère de convergence, même longueur de régularisation mécanique si utilisée.
• Point d’attention : cette méthode fournit une borne inférieure de l’incertitude de mesure. En effet, les conditions exactes de l’essai seront toujours différentes de celles de la prise d’images statiques . Si possible, il faut privilégier des configurations où la quantité d’intérêt est très grande devant le bruit de fond. Il peut être nécessaire d’adapter le dispositif expérimental (caméras plus résolue, focale plus longue) ou le modèle par éléments finis (éléments plus grossiers) afin de faire chuter l’incertitude sous le seuil souhaité pour l’application visée.

Et le biais ?

En règle générale, il est impossible de déterminer le biais précisément. En effet, la valeur « vraie » des quantités d’intérêt est inconnue et fait l’objet de la mesure. Cependant, il est possible d’exclure certaines sources de biais en réalisant quelques tests préalables à l’essai.

En complément de l’étude d’incertitude décrite dans la section précédente, une autre grandeur peut être intéressante. Ainsi, on peut regarder l’évolution de la moyenne de la quantité d’intérêt sur un ensemble d’images statiques. Une variation temporelle ou spatiale de cette moyenne sera le signe d’un biais imputable à un mouvement de caméra, à des vibrations dans le hall d’essai… Sources qu’il incombera à l’utilisateur de discriminer.

Dans le cas d’un post-traitement réalisé avec EikoTwin DIC, certains paramètres utilisateurs sont susceptibles d’introduire du biais dans la mesure. Le premier est le maillage par éléments finis utilisé pour réaliser la mesure. Si les éléments sont trop grands par rapport à la taille caractéristique du phénomène observé, cela introduit un lissage artificiel des résultats qui peut entraîner du biais. Ce n’est généralement pas le cas lorsque ce maillage est issu d’un calcul par éléments finis bien conçu. En effet, ce maillage est réalisé afin de décrire précisément le phénomène qu’on souhaite valider par l’expérience. Cependant, cela peut se produire dans le cas où l’on réalise le maillage spécifiquement pour la mesure. L’utilisateur doit quoi qu’il arrive garder un regard critique sur l’adéquation de son maillage à la description du phénomène observé. Dans le cas d’un maillage de mesure trop fin, il est nécessaire d’utiliser de la régularisation mécanique. On prendra alors garde à limiter la longueur de régularisation à quelques éléments, longueur au-delà de laquelle on est susceptible d’introduire du biais dans la mesure.

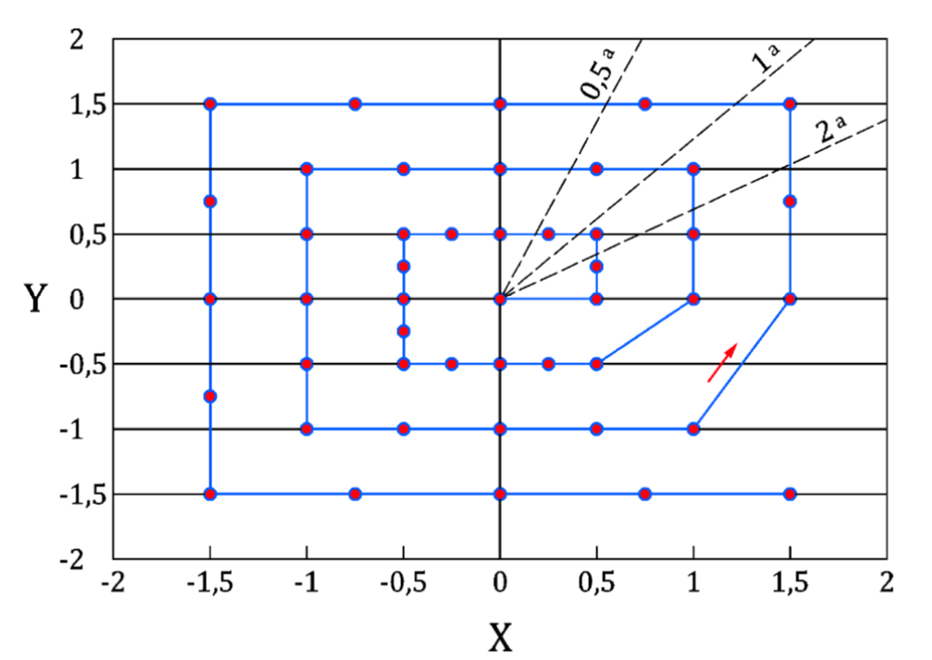
Enfin, parmi les efforts menés pour caractériser le biais en corrélation d’images numériques, on peut se référer à la norme ASD-STAN prEN 4861 P1 qui définit une procédure de mesure du biais. Le principe est d’appliquer une série de déplacements connus (Figure 2) à l’objet étudié et de déterminer le biais pour chaque position de l’objet, ce qui permet d’estimer la qualité de mesure pour l’ensemble du volume d’étude. Cependant, cette procédure ne peut généralement pas s’appliquer à un dispositif d’essai sur structures. En effet, il faut pouvoir déplacer précisément la pièce étudiée dans son environnement, ce qui limite l’adoption de cette norme dans la pratique.

Conclusion

La détermination pratique de l’erreur de mesure sur un essai de corrélation d’images numériques présente plusieurs défis spécifiques. Il faut retenir que l’erreur de mesure dépend de nombreux paramètres spécifiques à chaque essai. Nous reviendrons sur ces paramètres dans un prochain article de blog sur le sujet. Il est donc souhaitable d’acquérir une série d’images statiques avant chaque essai afin de déterminer l’amplitude du bruit de mesure. C’est la connaissance de ces amplitudes pour chaque dispositif expérimental qui déterminera le cadre d’une comparaison essai-calcul pertinente. Tout d’abord, il faut s’assurer que l’amplitude de la quantité simulée à valider est bien nettement supérieure au bruit de mesure. Dans un second temps, on ne peut mettre en évidence un écart significatif entre essai et simulation que lorsque l’écart entre quantités mesurées et calculées est supérieur au bruit de mesure.

Enfin, lors de la rédaction des rapports d’essai, il est important de bien documenter les démarches mises en œuvre pour quantifier les incertitudes et biais éventuels. Il faudra alors en tenir compte lors de l’interprétation les résultats de l’essai.