La régularisation mécanique sur EikoTwin DIC

• Par Lucas Angénieux, Ingénieur de recherche chez EikoSim

Sur le logiciel EikoTwin DIC, le calcul des champs de déplacements se fait sur le maillage de simulation. Cependant, ce problème mathématique étant par nature mal posé, il existe un paramètre de régularisation mécanique qui permet à l’utilisateur d’ajouter des conditions mécaniques aux mesures de champs. Contrairement à la plupart des logiciels de corrélation d’images numériques, chez EikoSim nous avons fait le choix d’utiliser un « filtre » mécanique afin de ne pas filtrer de façon artificielle mais en conservant un sens mécanique grâce à la régularisation. Nous allons voir dans cet article le sens de cette régularisation et ainsi fournir quelques recommandations quant à son utilisation.

Pourquoi ajouter de la régularisation mécanique ?

En corrélation d’images numériques, afin de calculer les champs de déplacements à partir d’un jeu d’images, on utilise les niveaux de gris d’une image de départ et d’une image d’arrivée pour suivre le déplacement entre les deux (plus d’informations dans ces articles sur les principes de la corrélation d’images numériques (CIN) et sur la méthode globale). Cette hypothèse de conservation des niveaux de gris permet de construire le problème de minimisation (1), mis sous forme matricielle :

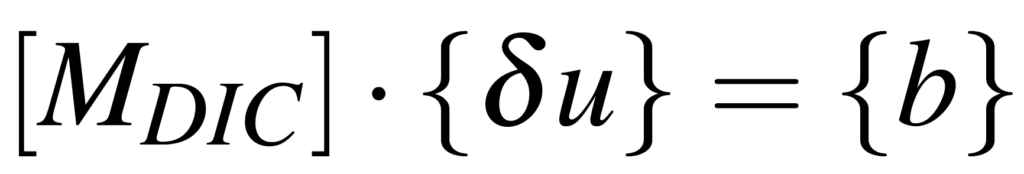
Le schéma de type Gauss-Newton utilisé pour résoudre ce problème présente de bonnes caractéristiques de convergence, mais risque de ne pas converger vers un résultat satisfaisant si la fonctionnelle comporte de nombreux plateaux ou des minima locaux : on dit que le problème est mal posé (cf. Figure 1). On va donc chercher un moyen de modifier la fonctionnelle pour permettre la convergence de l’algorithme en dépit de ces zones problématiques.

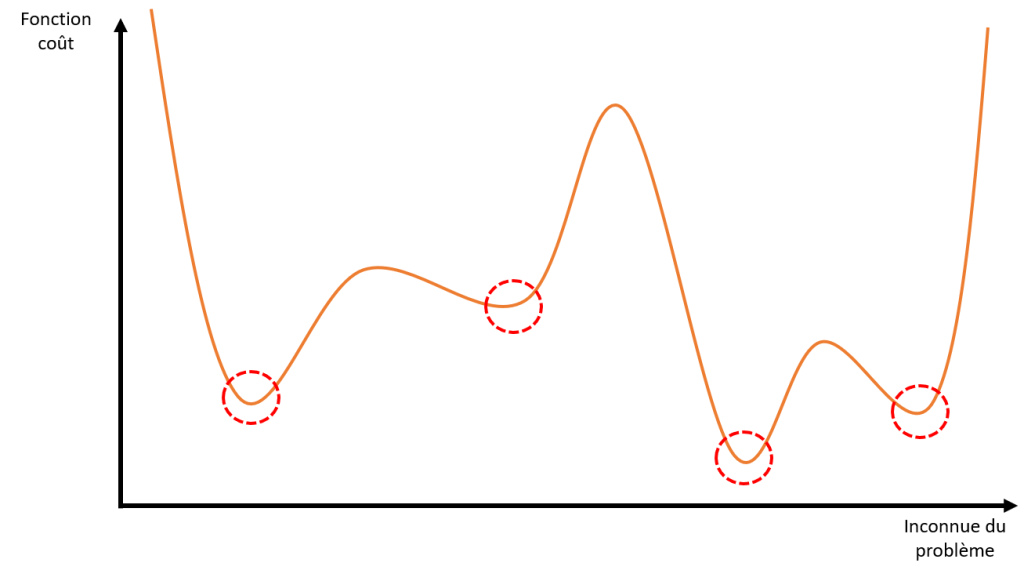
Une des solution utilisées pour résoudre des problèmes complexes est de faire appel à de la régularisation. Cette technique consiste à ajouter un terme de pénalisation à la fonctionnelle à minimiser, afin d’écarter les solutions qui satisfont le moins à certains critères attendus sur le champ résultat. Dans le cas de la régularisation mécanique, ce sont les champs de déplacements mécaniquement inadmissibles (par exemple trop « haute fréquence ») qui vont être pénalisés. Cette solution, qui agit comme une sorte de « filtre » mécanique, peut être proches des filtres utilisées dans la majorité des logiciels de CIN actuels, à ceci près qu’ici, seules des hypothèses mécaniques sont faites.

La régularisation mécanique dans EikoTwin DIC

Pour rajouter de l’information mécanique au problème, nous pouvons nous baser sur une loi de comportement solide, avec des hypothèses simplificatrices qui dépendent du matériau considéré. Excepté dans les cas d’un matériau architecturé ou multiphasique par exemple, on peut choisir la loi de Hooke en élasticité linéaire, homogène et isotrope (LHI) qui permettra de traiter fidèlement de nombreux cas industriels.

A l’aide de la loi de Hooke (2) ainsi que l’équilibre statique d’un solide (3), on modifie alors le schéma (1) sous la forme suivante (4) :

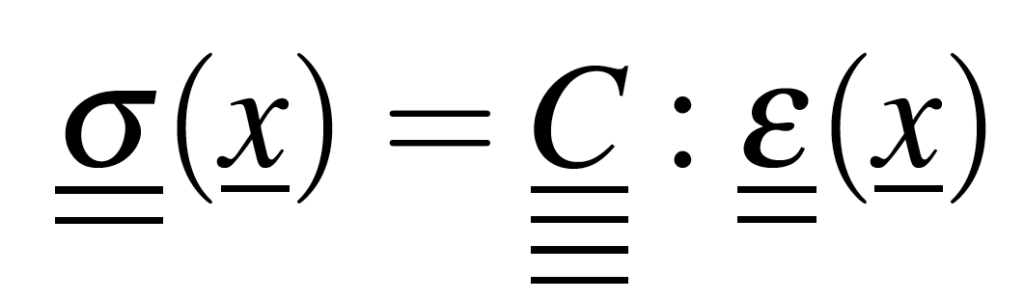
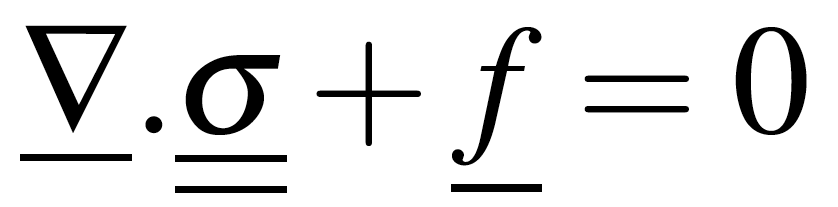
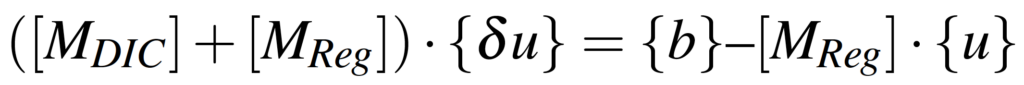
Ainsi, le nouveau système revient à minimiser une nouvelle fonctionnelle, combinaison linéaire de la fonctionnelle de corrélation d’images et de la fonctionnelle de régularisation (cf Figure 2). Une pondération doit être appliquée à ces deux fonctionnelles afin de se prémunir d’une influence trop importante de l’une de ces fonctionnelles sur le champ mesuré. C’est ici qu’intervient la longueur de régularisation à choisir par l’utilisateur dans EikoTwin DIC.

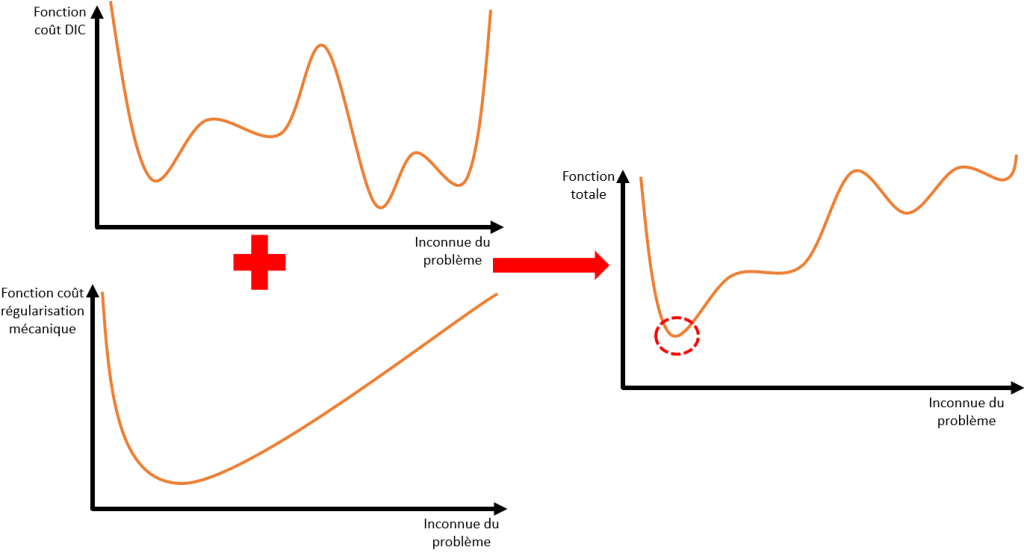
La longueur de régularisation sur EikoTwin DIC

Dans EikoTwin DIC, l’utilisateur choisit 3 paramètres lors de la mesure des champs de déplacements et de déformations : le nombre maximum d’itérations, le critère de convergence et la longueur de régularisation. Le choix de cette longueur a une influence sur les résultats ainsi que sur la vitesse de convergence. Il est alors nécessaire d’en comprendre le sens physique afin d’effectuer le meilleur choix possible.

Dans la suite de cet article, nous allons évoquer différents exemples. Ces exemples sont basés sur des images générées virtuellement, à l’aide du logiciel EikoTwin Virtual, un logiciel développé par EikoSim (voir l’article sur les essais virtuels avec EikoTwin Virtual pour plus d’explications). Ainsi, il nous est possible de générer des images pertinentes dont nous connaissons parfaitement la géométrie et les champs de déplacements et de déformations théoriques qui nous serviront de référence.

La longueur de régularisation vue comme la taille de la zone d’approximation locale à un modèle élastique linéaire

Comme nous avons pu le voir précédemment, la régularisation mécanique se base ici sur une loi de comportement : la loi de Hooke en élasticité linéaire, homogène et isotrope. Sans régularisation mécanique, le formalisme par éléments finis impose déjà une continuité du déplacement d’un nœud à l’autre, lors de la mesure. La régularisation permet d’ajouter une hypothèse mécanique à un ensemble de nœuds, localement. Ainsi, on peut voir la longueur de régularisation comme la dimension de la zone locale dans laquelle le modèle est approximé par un modèle élastique linéaire. Une longueur de régularisation trop importante limitera donc le mouvement de la pièce à un mouvement de corps rigide, tandis qu’une longueur de régularisation inférieure à la taille d’un élément n’aura absolument aucun effet.

Sur l’exemple de la Figure 3, on observe une pièce plane avec une marche de déplacements de 2 mm selon la normale à la pièce (sur le graphique de droite, la courbe en vert représente le profil de déplacement appliqué à la pièce sur les images virtuelles utilisées dans cet exemple). Ici, la longueur de régularisation appliquée (100 mm) peut être donc vue comme la longueur sur laquelle la marche de 0 à 2 mm sera mesurée. On observe ainsi sur le graphique de droite en bleu le profil de déplacement selon la normale, avec une « zone de transition » de 100 mm. Cette zone est en effet la zone dans laquelle l’effet de la loi de comportement élastique linéaire vue précédemment est effectivement visible.

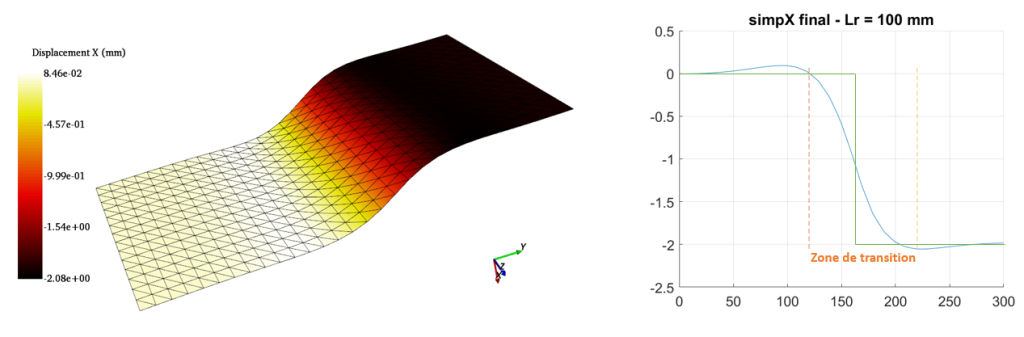
En pratique, il faudra alors faire attention à ne pas choisir une longueur de régularisation trop importante par rapport aux ordres de grandeurs que l’on cherche à mesurer, pour ne pas perdre l’information contenue dans la mesure initiale (sans longueur de régularisation).

La longueur de régularisation vue comme une fréquence de coupure d’un filtre passe-bas

On peut également voir la régularisation comme un filtre qui coupe les variations à haute fréquence du champ de déplacement. Dans ce contexte, la longueur d’onde associée à la fréquence de coupure est égale à la longueur de régularisation.

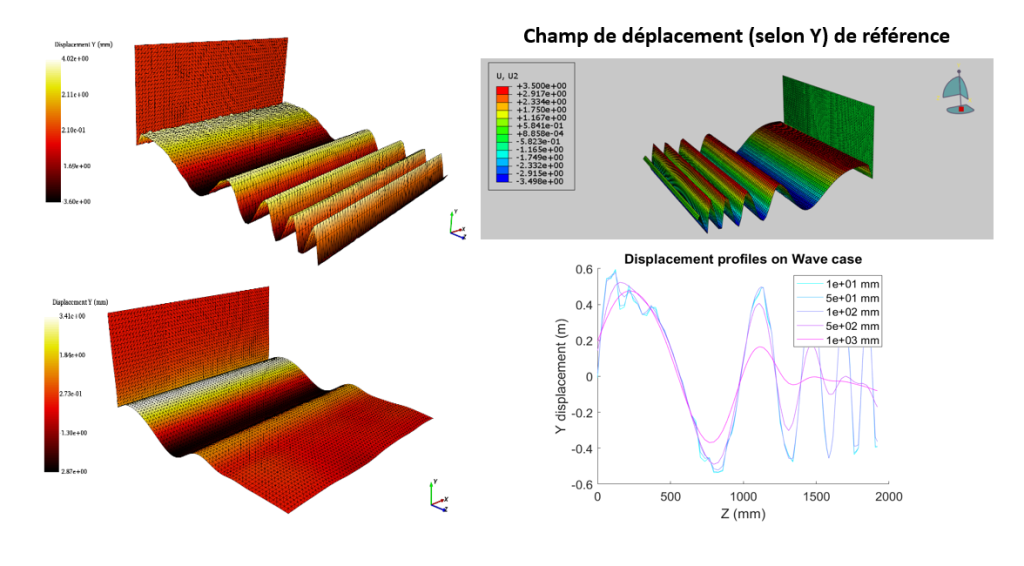
Une illustration pertinente de cette vision est présentée dans l’exemple qui suit. On observe ici le cas d’une maquette en L de longueur 2000 mm. On génère (à l’aide du logiciel EikoTwin Virtual) des images virtuelles de cette maquette en suivant le profil de la Figure 4 : un déplacement pseudo-sinusoïdal normale selon la direction Y, d’amplitude fixe et dont la longueur d’onde varie continûment de 100 mm à 1500 mm sur la longueur de la pièce. Les éléments ont une taille d’environ 60 mm.

On observe alors le champ mesuré pour des longueurs de régularisation mécanique différentes (de 50 mm en haut à 1000 mm en bas) sur la Figure 5. Comme attendu, la régularisation n’a aucun effet pour la longueur la plus faible (d’une valeur inférieure à la taille d’un élément ; le signal est bruité mais on observe toutes les fluctuations de déplacements). Pour la longueur de régularisation la plus élevée (correspondant à la moitié de la taille de la plaque), il n’y a plus de fluctuations très haute fréquence (« bruit ») à l’échelle de l’élément (voir en particulier la zone proche du plan vertical). Cependant, les longueurs d’ondes inférieurs aux 1000 mm sont nettement atténuées. Seule la vague de longueur d’onde supérieure à 1000 mm est correctement mesurée. A droite, on a tracé le profil de déplacement selon Y le long d’une ligne sur l’axe Z de la pièce. On peut alors observer les différents profils de déplacements selon les longueurs d’ondes utilisées, qui mettent en évidence le comportement de type filtre passe-bas de la régularisation.

Vers une vision plus mathématique de la régularisation mécanique

Une autre manière de voir l’influence et le poids de la régularisation mécanique dans le problème (4) peut s’illustrer sur la Figure 6 ci-dessous :

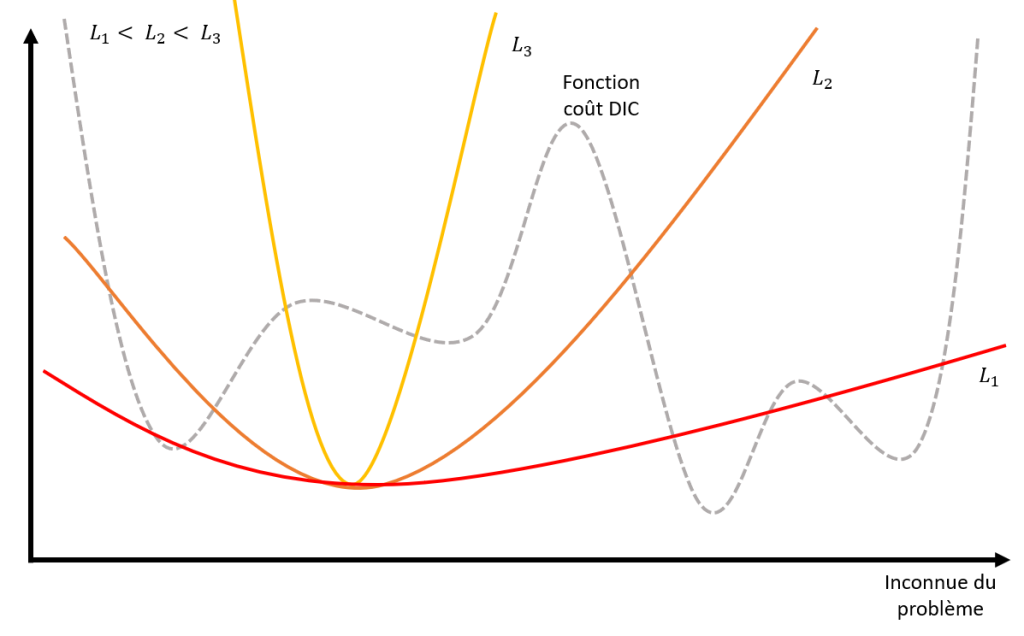
Sur la Figure 6, on voit que la longueur de régularisation a une influence sur la fonctionnelle de régularisation mécanique [1]. Ainsi, dans cet exemple, la longueur L₁ (trop faible) n’a que très peu d’influence sur la fonctionnelle globale, et il restera des minima locaux à droite qui ne correspondent pas à la solution, l’algorithme risque de ne pas converger correctement. Une longueur trop élevée L₃ va donner trop de poids à la régularisation mécanique, et va donc discriminer le minimum global solution. On voit donc que la longueur L₂ va déplacer les minima locaux de droite, et favoriser le minimum de gauche qui est solution.

Comment bien choisir la longueur de régularisation mécanique ?

Il est important de noter que la longueur de régularisation dépend du cas traité (maillage, zone de mesure, phénomène à observer, etc…) et il n’existe donc pas de longueur « idéale » dans l’absolu. Il revient à l’utilisateur de choisir la longueur de régularisation la plus adaptée à son cas, en effectuant le meilleur compromis entre vitesse de calcul, convergence et niveau de détails (c’est-à-dire richesse du champ de déplacement). Cet article permet dans un premier temps de mieux comprendre l’effet de la régularisation mécanique sur le champ solution ainsi que le sens physique de la longueur à appliquer.

Pour illustrer cette partie, nous nous intéresserons aux déformations mesurées sur des images virtuelles d’une éprouvette de traction classique, de longueur 95 mm et maillée avec des éléments de taille 2 mm dans la zone d’intérêt. Le champ de déformation de référence le long de l’axe de traction (utilisé pour la génération des images) est présenté sur la Figure 7 ci-dessous.

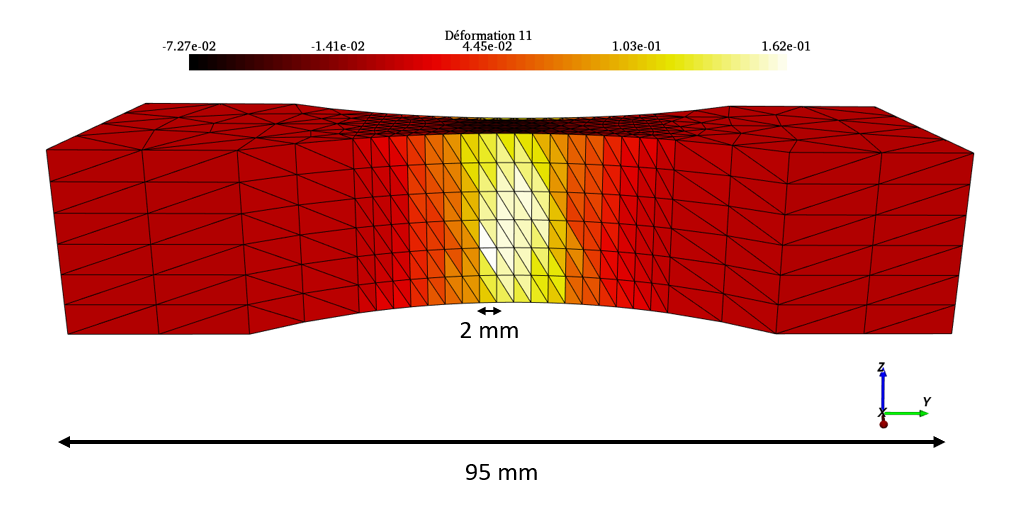
Chez EikoSim, nous recommandons dans un premier temps de réaliser une mesure sans longueur de régularisation. Cela fournit des résultats préliminaires, sans aucun effet de régularisation mécanique. Dans un second temps, une longueur de régularisation de la taille de 2 ou 3 éléments peut être pertinente pour améliorer la convergence en s’affranchissant du bruit de mesure. Une analyse de l’effet de la longueur de régularisation sur une grandeur d’intérêt en particulier (capteurs de déplacements, jauges de déformations) ou bien sur les champs (déplacements, déformations, résidus de corrélation) peut également permettre d’affiner ce choix. C’est ce que nous allons effectuer sur le cas de l’éprouvette. Au vu des sollicitations et de nos images, il est plus pertinent de s’intéresser aux résidus ainsi qu’aux déformations au milieu de l’éprouvette, plutôt qu’aux champs de déplacements.

Les champs de résidus sont un bon outil pour juger du choix d’une longueur de régularisation. L’utilisateur peut lancer différents calculs en faisant augmenter la longueur de régularisation, et étudier son influence sur le champ de résidus (l’utilisation du plugin Mode Batch peut ici être particulièrement pertinente). A partir d’une certaine valeur, la longueur de régularisation fera augmenter les résidus, particulièrement dans les zones ou la pièce se déforme le plus. En effet, le champ de déplacement solution va s’apparenter à un mouvement de corps rigide, et dans ce cas la contribution du terme de régularisation dans la fonctionnelle globale sera disproportionnée. On peut donc étudier à partir de quelle valeur on observe cette augmentation locale des résidus, particulièrement dans les zones d’intérêts de notre essai. Sur notre exemple, on peut voir Figure 8 qu’à partir d’une longueur de régularisation de 15 mm les résidus augmentent, et explosent même après 30 mm, signe d’une très mauvaise mesure du champ de déplacements. Il convient donc de choisir une longueur entre 0 et 10 mm (soit entre 0 et 5 éléments).

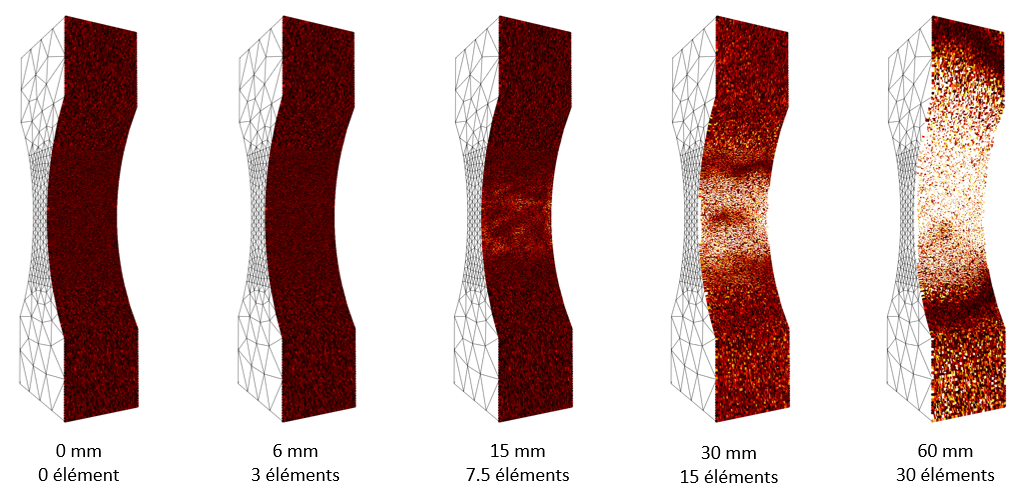
On peut également observer le profil de déformation en traction le long de l’éprouvette (en traçant à un temps fixé la déformation selon l’axe de traction sur un profil) sur la Figure 9. On remarque, conformément aux explications sur l’effet de la régularisation vues plus haut, l’influence de la longueur de régularisation choisie par l’utilisateur sur les mesures faites sur EikoTwin DIC. A partir d’une longueur de régularisation trop importante, les champs vont être lissés et écrasés, ainsi la déformation mesurée le long du profil va diminuer. Ces profils confirment le choix d’une longueur de régularisation de 6 mm (soit 3 éléments) par rapport à une longueur de régularisation de 15 mm. Ce cas permet bien d’illustrer l’intérêt de la régularisation (un filtrage des hautes fréquences parasitant les résultats d’essais), tout en montrant bien l’impact négatif que peut avoir le choix d’une longueur trop élevée. Une attention particulière doit donc être portée au choix de la longueur de régularisation, pour effectuer le meilleur compromis possible entre vitesse et convergence du calcul et niveau de détail de la mesure.

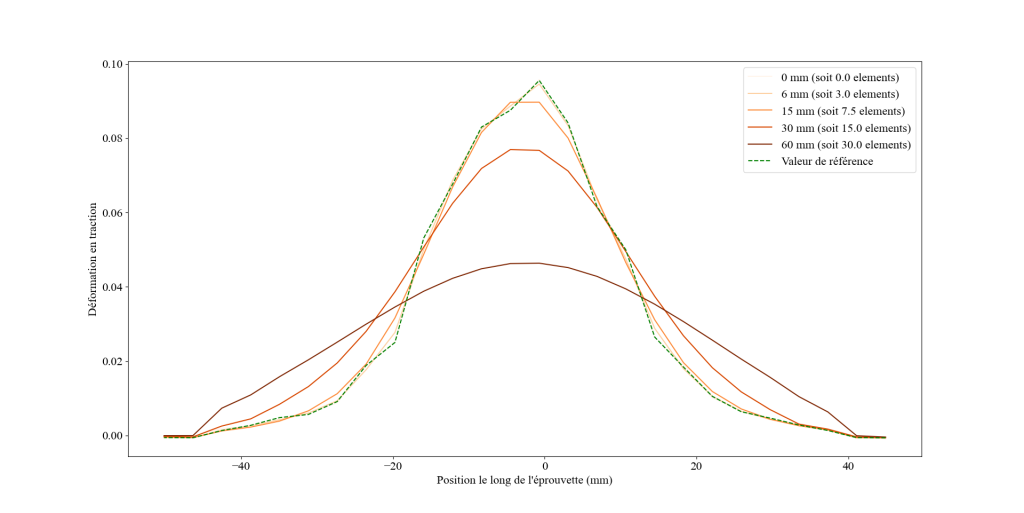
Conclusion

Dans cet article, nous avons pu voir que la régularisation mécanique sur le logiciel EikoTwin DIC est un outil mathématique qui impose une condition mécanique à la mesure des champs par corrélation d’images numériques. Elle permet ainsi de corriger des erreurs qui peuvent exister lors de certains essais : maillage de simulation trop fin, mouchetis non adapté à la taille du maillage, bruit de mesure trop important qui empêche une interprétation correcte des résultats, etc…

Les différentes approches physiques ou mathématiques de la longueur de régularisation aident à mieux appréhender son utilisation afin d’obtenir d’excellents résultats lors des essais. En pratique, une première analyse sans régularisation, puis une évolution progressive de cette longueur en regardant les quantités d’intérêts propres à l’essai permettent de choisir la longueur de régularisation adaptée. Une longueur égale à la taille de 2 ou 3 éléments se révèle en général bien adaptée à la plupart des cas.

Références bibliographiques

[1] Arturo Mendoza, Jan Neggers, François Hild, Stéphane Roux. Complete Mechanical Regularization
Applied to Digital Image and Volume Correlation. Computer Methods in Applied Mechanics and
Engineering, Elsevier, 2019, 355, pp.27-43. 10.1016/j.cma.2019.06.005 . hal-02148780, Complete Mechanical Regularization Applied to Digital Image and Volume Correlation – Archive ouverte HAL (archives-ouvertes.fr)