Etalonnage d’une caméra : principes et procédures
- Par Myriam Berny, Ingénieure R&D chez EikoSim
L’utilisation d’un système multi-caméras pour faire de la métrologie et effectuer des mesures précises nécessite de réaliser un étalonnage de ces caméras. Celles-ci peuvent être représentées mathématiquement par un modèle de projection, sous la forme d’une matrice, permettant le passage de la position de points 3D vers leur projection dans l’espace image 2D. Le processus d’estimation des paramètres du modèle de caméra, consistant en un jeu de paramètres intrinsèques et un jeu de paramètres extrinsèques, est connu sous le nom d’étalonnage.
Dans la suite, on présentera tout d’abord le modèle mathématique décrivant une caméra, puis les grandes familles de méthodes d’étalonnage utilisées en vision assistée par ordinateur, et enfin les précautions à prendre pour limiter les erreurs commises lors de l’étalonnage et garantir son succès.
Comment modéliser une caméra ?
Le modèle géométrique d’une caméra, représentée en Figure 1, est basé sur trois transformations élémentaires. Leur combinaison forme ce qu’on appelle le modèle sténopé [1].
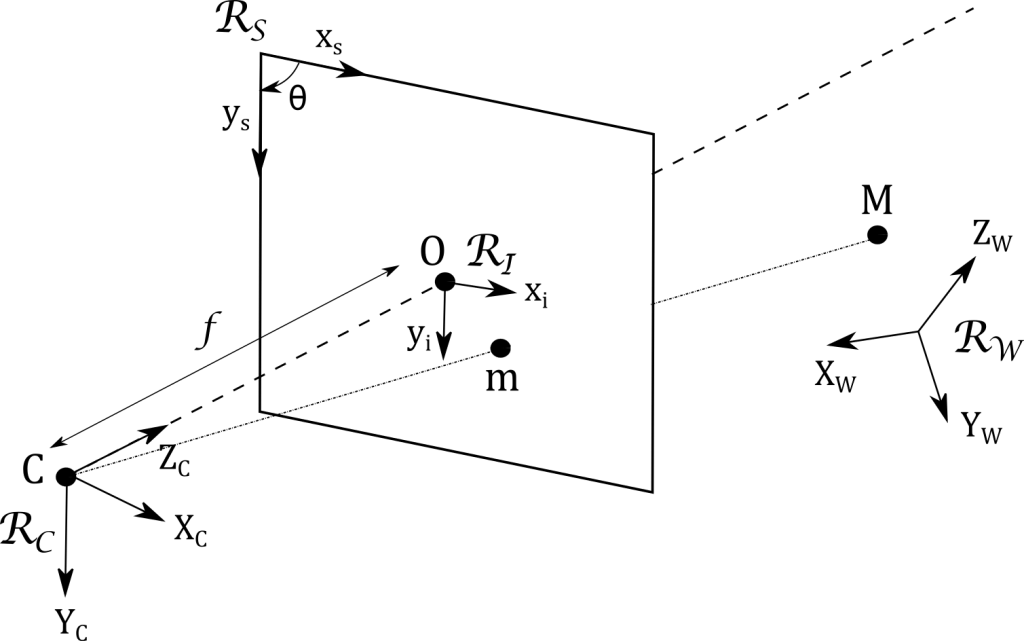
La position d’un point 3D M de la scène, définie dans le repère monde Rw par ses coordonnées (XW, YW, ZW), est exprimée dans le repère local Rc attaché à la caméra C avec les coordonnées locales (XC,YC,ZC). Ce changement de repère constitue la première transformation et ne dépend que de trois rotations et de trois translations. Cette première transformation entre les coordonnées homogènes monde {XW} = {XW, YW, ZW,1} et les coordonnées homogènes locales {XC} = {XC, YC, ZC,1} est représentée par une matrice 4×4 notée T. Elle peut être décomposée en une matrice de rotation R (paramétrable par exemple par trois angles de rotation) et un vecteur de translation t (définie par trois composantes). On a donc :
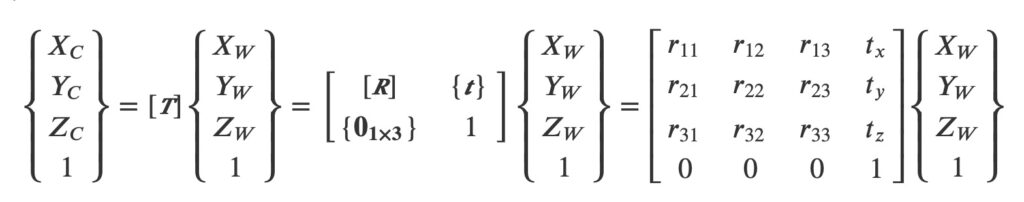
Ces six paramètres (trois angles, trois translations) sont appelés paramètres extrinsèques et définissent donc le positionnement de la caméra dans l’espace 3D.
La deuxième transformation correspond à la projection du point 3D M sur le plan image auquel est attaché le repère local RI en un point 2D m. Elle fait intervenir uniquement la focale f de la caméra et un facteur d’échelle s selon :
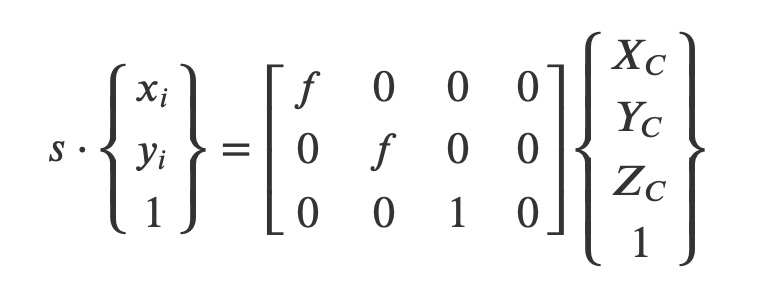
La dernière transformation exprime les coordonnées 2D homogènes {xs} = {xs ys, 1}T du point projeté m dans le repère du capteur RS et fait intervenir les caractéristiques du capteur :
- l’angle de décadrage entre les axes horizontaux et verticaux du capteur (« skew »), supposé égal à 90° ;
- la position du centre optique ;
- la taille physique du pixel dans les deux directions.
La combinaison des deux précédentes transformations peut être décrite à travers une matrice de projection 3×4 K qui s’écrit :
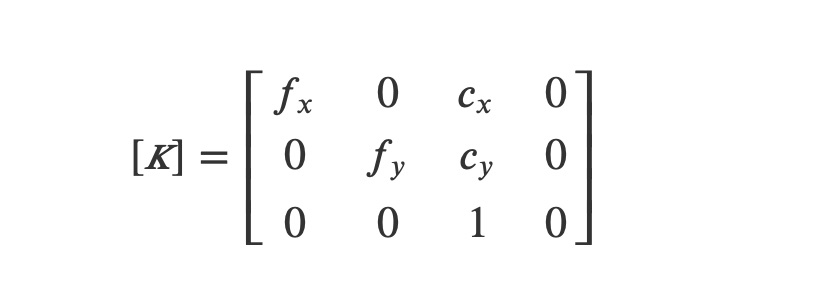
Cette matrice de projection est donc définie par quatre paramètres intrinsèques à la caméra étalonnée : les longueurs de focale horizontale fx et verticale fy en pixels et la position (cx,cy) en pixels du centre optique dans l’image.
La matrice de projection complète M décrivant une caméra est donc composée d’une matrice de paramètres extrinsèques T et d’une matrice de paramètres intrinsèques K, de sorte que :
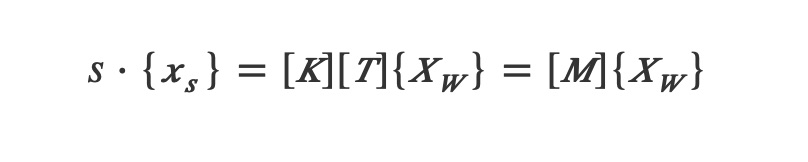
La matrice de projection M peut ainsi être exprimée de façon « implicite » comme une matrice 3×4 contenant 12 termes (mij) ou bien de façon « explicite », via les 10 paramètres indépendants extrinsèques et intrinsèques présentés précédemment. Sous sa forme explicite, M s’écrit alors :
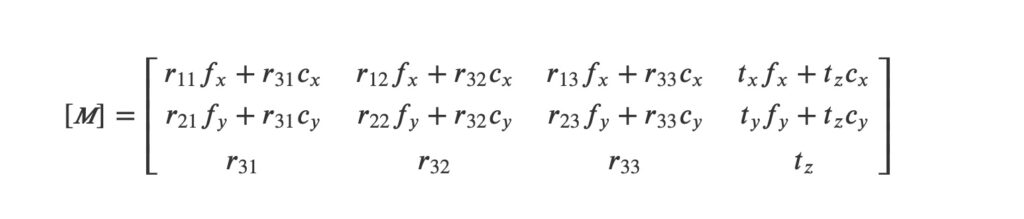
L’étalonnage d’une caméra a pour but d’estimer sa matrice de projection M. Lorsque la procédure vise à identifier les termes mij, on parle d’étalonnage implicite, tandis qu’on parle d’étalonnage explicite (ou étalonnage « fort ») lorsqu’elle permet d’identifier les paramètres extrinsèques et intrinsèques.
Dans le modèle de caméra introduit précédemment, les distorsions ne sont pas prises en compte. Les distorsions, qui sont dues aux imperfections du système optique telles que des défauts de forme et de positionnement des lentilles des caméras, vont dévier les faisceaux lumineux et donc induire un écart de positionnement pour le point projeté par rapport à un modèle idéal [2]. Il est possible alors de compléter le modèle de caméra en y introduisant les trois distorsions qui génèrent le plus d’effets, à savoir les distorsions radiales, de décentrage et prismatiques (voir Figure 2), induites par des défauts de courbure, de parallélisme des lentilles et de coaxialité des axes optiques.
 |  |  |  |  |
| (a) | (b) | (c) | (d) | (e) |
Dans la section suivante, on présentera les grandes familles de procédures d’étalonnage qui visent à déterminer les paramètres du modèle de caméra.
Comment réaliser l’étalonnage d’une caméra ?
Le but de l’étalonnage d’une caméra est de déterminer les paramètres (explicites ou implicites) de la matrice de projection qui lui est associée. Plusieurs méthodes existent qui peuvent être regroupées en trois grandes catégories, décrites ci-dessous :
- L’étalonnage par mire, qui constitue l’approche classique pour étalonner une caméra ;
- L’auto-étalonnage, qui utilise la connaissance a priori de la géométrie nominale de l’objet imagé pour déterminer les paramètres modélisant la caméra ;
- L’étalonnage hybride, qui allie les deux approches précédentes pour identifier séparément les paramètres intrinsèques et extrinsèques de la caméra.
L’étalonnage par mire est donc basé sur l’utilisation d’un objet 3D de géométrie bien connue (appelé mire d’étalonnage) et son image acquise par la caméra [1, 2]. Cette mire présente sur sa surface des points 3D spécifiques, de positions connues. Ils peuvent correspondre à l’intersection de lignes verticales et horizontales quand la mire est une grille (ou un damier) ou bien au centre de cercles lorsque la mire est composée de points. La position de ces points 3D sur l’image de la mire est souvent obtenue via des procédures automatiques d’analyse d’images [4].
 |  |  |  |
L’algorithme utilisé par cette approche vise alors à trouver les paramètres du modèle de caméra qui minimisent l’écart entre la position des points 3D projetés à l’aide du modèle de caméra et la position réelle de ces points sur l’image. L’algorithme consiste ainsi à optimiser la matrice de projection jusqu’à minimiser la somme quadratique de ces erreurs de reprojection. Avec ce type d’approche, la matrice de projection peut être identifiée soit de façon implicite, soit de façon explicite, et peut également inclure des modèles de distorsions pour les modèles les plus complexes [9, 10]. Dans le cas d’un système de stéréovision (c’est-à-dire à 2 caméras), cette approche va identifier de façon indépendante les paramètres (intrinsèques et extrinsèques) d’une des deux caméras, qui deviendra la « caméra maître » [5]. La seconde caméra, dite « caméra esclave », aura ses paramètres intrinsèques identifiés via l’image de mire et ses paramètres extrinsèques seront définis par rapport à la position de la caméra maître, à travers la détermination d’une matrice de transformation linéaire permettant de passer de la caméra 1 à la caméra 2. Cette matrice peut être prédéfinie par le fournisseur de systèmes de stéréovision pour des systèmes où la position relative des caméras est fixée, ou réidentifiée à partir des images de mires. Les mires utilisées devant occuper un espace 3D, elles doivent être 3D ou bien, si elles sont planes, être déplacées dans l’espace selon des mouvements de translation et rotation [1, 11]. Avec ce type d’étalonnage, il est nécessaire de réaliser au moins une cinquantaine d’images de mire [12, 13] pour espérer pouvoir étalonner le système de stéréovision et minimiser l’effet du bruit d’acquisition et des erreurs d’étalonnage. De plus, la mire étant extérieure, il n’est pas possible de réétalonner les caméras au cours de l’essai, ce qui peut s’avérer nécessaire si les caméras bougent par inadvertance (déplacement des pieds de caméras, dévissage progressif des caméras…).
Le second type d’étalonnage est appelé auto-étalonnage [14] et est utilisé en particulier par les approches de stéréocorrélation dites « globales » [15], comme celle proposée par EikoTwin DIC. Il utilise la pièce à tester dans son intégralité comme objet d’étalonnage et cela grâce à une description dense de l’objet (c’est-à-dire que la position de chaque point de la pièce est paramétrisée et peut être déterminée via un modèle mathématique [16]). Parmi les descriptions possibles, on trouve celle du maillage par éléments finis [17, 18]. Ainsi, l’intégralité du maillage est utilisée comme points spécifiques pour minimiser les erreurs de reprojection et identifier les paramètres des modèles de caméra (et non plus uniquement les points particuliers d’une mire). A l’intégralité de ce maillage sera associée la totalité de la pièce mouchetée visible sur les images acquises par les caméras, et par extension toute la richesse de la texture de la pièce (mouchetis). La procédure a ainsi pour but de trouver simultanément les paramètres implicites paramétrisant les caméras (sans hiérarchisation entre les caméras), en minimisant l’écart en niveau de gris entre la projection des points 3D via chacune des caméras (à l’aide de son modèle de projection à optimiser) et une image de référence commune à toutes les caméras (construite à partir de toutes les caméras). Les points 3D correspondent à des points d’évaluation construits pour chaque élément du maillage (subdivisions équiréparties au sein de l’élément) où les niveaux de gris et gradients seront évalués pour minimiser les erreurs de reprojection. Ainsi, avec cette approche, il est possible d’étalonner un système de stéréovision avec une seule paire d’images tout en étant robuste au bruit grâce à la multiplicité des points d’évaluation induite par la description dense de la pièce d’essai. Par ailleurs, la position des caméras est exprimée dans le repère de la pièce et l’étalonnage étant basée sur cette dernière, il est possible de réétalonner à volonté les caméras au cours de l’essai en utilisant les images acquises.
En revanche, l’une des limitations de cette approche par auto-étalonnage réside dans le caractère tridimensionnel de la pièce à tester, qui reste une condition pour éviter les singularités mathématiques de l’étalonnage d’une caméra [9]. Pour les cas où la pièce ne respecte pas ces conditions géométriques (cas d’une pièce plane ou d’un solide de révolution tel que le cylindre), il est recommandé de procéder à un étalonnage dit « hybride », qui est également une procédure proposée par EikoTwin DIC. Cette approche permet de combiner l’utilisation d’une mire de type ChAruCo (de géométrie bien connue) et une approche de stéréocorrélation globale (par auto-étalonnage). L’utilisation de la mire ChAruCo permet de fixer de façon explicite une partie des paramètres de projection, à savoir les paramètres intrinsèques de la caméra (matrice K), et de fiabiliser l’identification de la matrice extrinsèque T (sous forme implicite) par auto-étalonnage. Pour plus de détails, la description de cette approche, ses avantages et conditions d’application est présentée dans l’article « L’étalonnage hybride : une alternative robuste à l’auto-étalonnage » présent sur notre blog.
Que faire pour éviter les erreurs d’étalonnage d’une caméra ?
Lorsque les caméras ont mal été étalonnées, cela induit très souvent des erreurs de mesures de déplacements et, par conséquence, de déformations. Pour s’assurer d’un bon étalonnage, il peut alors être pertinent de réaliser une acquisition d’images de mouvements de corps rigide (translation) d’amplitude connue et de vérifier que la mesure de déplacements est cohérente.
Par ailleurs, plusieurs précautions peuvent être prises pour s’assurer de la réussite de la phase d’étalonnage :
- Faire du « Virtual Testing », en préparant l’essai en amont de façon virtuelle. Le logiciel EikoTwin Virtual, qui utilise l’outil de visualisation Blender, permet ainsi d’étudier en amont le positionnement des caméras et de l’optimiser afin d’avoir un bon étalonnage pour mesurer les déplacements attendus (à partir d’une simulation par éléments finis). Plus de détails concernant ces aspects sont disponibles dans l’article « Préparer votre essai de Corrélation d’Images Numériques avec Blender » disponible sur notre blog.
- Si cette phase de virtualisation de l’essai n’a pas pu être faite, il est conseillé d’anticiper les problèmes éventuels en adaptant la position des caméras le jour de l’essai, en ajoutant des points 3D dans le champ de vue ou encore en passant par un étalonnage hybride afin de fiabiliser l’étalonnage des caméras. Plusieurs critères ont été identifiés pour estimer en amont la fiabilité de l’étalonnage et sont présentés dans notre article « Maîtriser l’auto-étalonnage avec Eikotwin DIC ».
Conclusions
L’étalonnage des caméras constitue ainsi la première étape de toute analyse par corrélation d’images numériques et demeure une étape à réaliser méticuleusement, en particulier lorsque des mesures précises sont recherchées (de forme, de déplacements ou de déformations). Toutes les approches existantes visent à minimiser les erreurs de reprojection entre une caractéristique liée à la projection de points spécifiques 3D (position, valeur de niveau de gris) et leur caractéristique réelle sur l’image. Ces points peuvent alors être des points remarquables sur une mire ou des points d’évaluation associés à un maillage surfacique dans le cas des approches globales. EikoTwin DIC propose ainsi des procédures d’étalonnage par auto-étalonnage et par étalonnage hybride afin d’identifier de façon robuste et simultanée les matrices de projection des caméras en utilisant une seule paire d’images (et une vingtaine d’images de mire si l’étalonnage hybride est choisi). Ces procédures présentent ainsi de nombreux avantages (simplicité de la procédure, étalonnage dans le repère de la pièce testée, robustesse au bruit, possibilité d’étalonner simultanément un système multi-vues…) et permettent de s’adapter à tout type d’essai. En préparant en amont l’essai par virtualisation ou en vérifiant le respect de certains critères, il est alors possible de s’assurer d’un bon étalonnage des caméras qui reste un prérequis pour une mesure fiable des déplacements et la réduction des sources d’erreurs pour ces mesures cinématiques.
Références bibliographiques
[1] O. Faugeras, Three-dimensional computer vision: a geometric viewpoint. Cambridge, MA (USA) : MIT Press, 1993.
[2] M. Sutton, J. Orteu, et H. Schreier, Image correlation for shape, motion and deformation measurements: Basic Concepts, Theory and Applications. New York, NY (USA) : Springer, 2009.
[3] G. Besnard, Caractérisation et quantification de surfaces par stéréocorrélation pour des essais mécaniques du quasi statique à la dynamique ultra-rapide. Thèse de doctorat, ENS de Cachan, 2010.
[4] P. Brand, Reconstruction tridimensionnelle d’une scène à partir d’une caméra en mouvement : de l’influence de la précision. Thèse de doctorat, Université Claude Bernard (Lyon I), 1995.
[5] D. Garcia, Mesure de formes et de champs de déplacements tridimensionnels par stéréocorrélation d’images. Thèse de doctorat, Institut National Polytechnique de Toulouse (INPT), 2001.
[6] J. Heikkilä, “Geometric camera calibration using circular control points”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, pp. 1066 – 1077, 2000.
[7] Original image from: https://dantecdynamics.com/wp-content/uploads/2019/11/2.-Calibration-target.png
[8] Original image from: https://correlatedsolutions.com/wp-content/uploads/2016/09/3D-Calibration.jpg
[9] R. Tsai, “A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses”, IEEE J. Robotics Autom., vol. RA- 3, no. 4, pp. 323–343, 1987.
[10] J. Heikkilä et O. Silvén, “A four-step camera calibration procedure with implicit image correction”, IEEE International Conference on Computer Vision and Pattern Recognition, pp. 1106–1111, 1997.
[11] Z. Zhang, “A flexible new technique for camera calibration”, IEEE Trans. Pattern Anal. Machine Intell., vol. 22, no. 11, pp. 1330–1334, 2000.
[12] M. Sutton, “Computer vision-based, noncontacting deformation measurements in mechanics: A generational transformation”, Appl. Mech. Rev., vol. 65, no. AMR-13-1009, p. 050802, 2013.
[13] International Digital Image Correlation Society, A Good Practices Guide for Digital Image Correlation, Jones, E.M.C. et Iadicola, M.A. (Eds.), 2018.
[14] O. Faugeras, Q. Luong, et S. Maybank, “Camera self-calibration: Theory and experiments”, dans Proc. 2nd ECCV, pp. 321–334, Springer-Verlag, 1992.
[15] J.-E. Dufour, F. Hild, et S. Roux, “Shape, Displacement and Mechanical Properties from Isogeometric Multiview Stereocorrelation”, J. Strain Analysis, vol. 50, no. 7, pp. 470–487, 2015.
[16] F. Hild et S. Roux, “Procédé de mesures tridimensionnelles par stéréo-corrélation utilisant une représentation paramétrique de l’objet mesuré”, Déc. 6 2013. Brevet n°FR2991448.
[17] J.-E. Dufour, B. Beaubier, S. Roux, et F. Hild, “Displacement measurement using CAD-based stereo-correlation with meshes”, dans ICEM conference, 2014.
[18] L. Dubreuil, J.-E. Dufour, Y. Quinsat, et F. Hild, “Mesh-Based Shape Measurements with Stereocorrelation: Principle and First Results”, Exp. Mech., no. 56, pp. 1231–1242, 2016.

98-100 AVENUE ARISTIDE BRIAND
92120 MONTROUGE
FRANCE


