L’analyse modale est une technique clé utilisée en ingénierie pour comprendre les comportements vibratoires des structures mécaniques. Elle permet de déterminer les fréquences naturelles et les formes modales d’une structure, des éléments cruciaux pour s’assurer que celle-ci ne résonne pas dangereusement sous des conditions de fonctionnement spécifiques.
Traditionnellement, cette analyse repose sur l’utilisation d’accéléromètres ponctuels, qui fournissent des résultats partiels sur les formes modales des structures. Par sa capacité à fournir des mesures de champs, la Corrélation d’Images Numériques (ou Digital Image Correlation – DIC) ouvre d’autres perspectives pour cette analyse vibratoire.
L’objectif de cet article est d’évaluer la possibilité de déterminer les formes et les fréquences modales d’une structure à l’aide de la DIC. Pour cela, des données de test synthétiques ont été générées et exploitées dans l’objectif de valider la méthode proposée dans un environnement contrôlé avant de l’appliquer à des cas industriels concrets. L’article présente la démarche de génération d’images virtuelles avec un champ de référence calculé par éléments finis, puis les résultats de cette étude.
Simulation d’un comportement vibratoire par la méthode des éléments finis
Un modèle de maquette d’aile d’une longueur de 600 mm fixé à sa base a été utilisé pour cette étude. A l’aide du solveur Abaqus, les cinq premiers modes du modèle ont étés déterminés (cf. Figure 1).
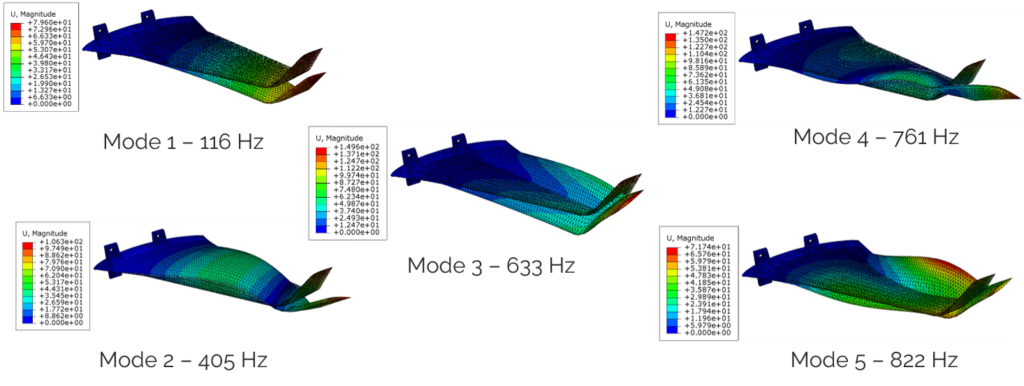
Les amplitudes maximales calculées des modes n’ayant pas de sens physique, différents facteurs d’échelle ont été appliqués aux cinq modes spatiaux dans l’objectif d’appliquer des déplacements réalistes au modèle (cf. Figure 2).
Pour chacun des champs modaux, une amplitude sinusoïdale a été générée pour une durée de 30 ms, soit environ trois fois la fréquence de vibration du premier mode. Selon le théorème de Shannon, la fréquence d’échantillonnage doit être supérieure à deux fois la fréquence maximale présente dans le signal. Pour tenir compte des erreurs de mesure, une fréquence d’échantillonnage de 5000 Hz a été utilisée, soit environ six fois la fréquence vibratoire du cinquième mode. La Figure 3 présente ces courbes d’amplitude pour un nœud situé sur le winglet.
Ces champs ont été additionnés pour chaque nœud afin de générer un comportement vibratoire qui contient une contribution de l’ensemble des cinq modes. La Figure 4 illustre cette superposition pour un nœud situé sur le winglet.
Génération d’images virtuelles pour l’analyse vibratoire avec l’outil EikoTwin Virtual
L’outil EikoTwin Virtual, basé sur le logiciel Blender, permet de générer des images photoréalistes à partir d’un modèle éléments finis et des caractéristiques et des positions des caméras utilisées (cf. Figure 5). Des caméras de résolution 1280 x 960 px avec un objectif de 25 mm situées à une distance d’environ 800 mm de la pièce ont été modélisées. A partir de l’analyse vibratoire générée précédemment, le modèle élément fini a été déformé et des séries d’images ont été exportées constituant ainsi des données de test synthétiques pour la DIC.
Mesure de champs de déplacement avec l’outil EikoTwin DIC
L’outil EikoTwin DIC permet de mesurer des champs de déplacement par corrélation d’images numériques directement sur un maillage éléments finis. A partir des images synthétiques générées précédemment, les déplacements de l’aile en vibration ont été mesurés sur sa surface supérieure (cf. Figure 6). L’application d’un bruit sur l’image de référence a permis d’estimer l’incertitude de mesure à 5 microns, soit un cinquième de l’amplitude du cinquième mode.
La Figure 7 présente la comparaison entre le comportement vibratoire donné en entrée (U Input) et le comportement vibratoire mesuré avec EikoTwin DIC (U DIC) pour un nœud situé sur le winglet.
Détermination des modes par SVD et des fréquences associées par FFT
La méthode de Décomposition en Valeur Singulières ou Singular Value Decomposition (SVD) a été appliquée à l’ensemble du champ de déplacement mesuré par DIC pour estimer les cinq premiers modes. Cette méthode permet d’approximer un ensemble de données en le décomposant en trois ensembles de rang inférieur. Dans ce cas, le premier ensemble correspond aux modes temporels, chacun d’eux est associé à une densité spectrale (deuxième ensemble), et à un mode spatial (troisième ensemble). La Figure 8 présente une comparaison entre les 5 premiers modes spatiaux utilisés pour générer le cas synthétique et ceux mesurés, chacun à amplitude temporelle maximale.
La Figure 9 présente pour chaque mode et chaque direction une comparaison du signal sinusoïdal d’entrée (Input) avec les modes temporels obtenus par SVD pour un nœud situé sur le winglet (DIC-SVD).
La méthode de Transformation de Fourier Rapide ou Fast Fourier Transformation (FFT) a été appliquée à chaque mode temporel obtenu par SVD à partir de l’ensemble du champ mesuré par DIC pour estimer les fréquences des cinq premiers modes. Le tableau ci-dessous présente pour chaque mode une comparaison des fréquences propres d’entrée avec les fréquences propres estimées par FFT pour une fréquence d’échantillonnage de 5000 Hz ainsi que pour une fréquence d’échantillonnage de 2000 Hz (plus proche de la condition limite du théorème de Shannon).
| Mode | Input (Hz) | DIC-SVD-FFT (5000 Hz) | DIC-SVD-FFT (2000 Hz) |
| 1 | 116 | 117 | 125 |
| 2 | 405 | 410 | 406 |
| 3 | 633 | 645 | 656 |
| 4 | 761 | 762 | 781 |
| 5 | 822 | 820 | 844 |
Résultats de l’analyse vibratoire
Les modes spatiaux déterminés à l’aide de la DIC et la SVD présentent une tendance très similaire aux modes spatiaux d’entrée. Les fréquences modales déterminées à l’aide de la DIC, la SVD et la FFT ont montré une très bonne concordance avec celles issues des simulations FEM. Par exemple, pour le premier mode, la fréquence calculée par FEM était de 116 Hz, tandis que celle déterminée par DIC était de 117 Hz, démontrant ainsi la précision de la méthode. Cette précision s’est maintenue pour les autres modes.
L’étude a été menée à la fois avec une fréquence d’échantillonnage de 5000 Hz, soit environ six fois la fréquence propre maximale de la sélection, ainsi qu’avec une fréquence d’échantillonnage de 2000 Hz (soit deux fois la fréquence propre maximale). Les fréquences propres identifiées ont montré une dégradation, ce qui était attendu conformément à la condition du théorème d’échantillonnage de Shannon.
Conclusion
Cette étude a permis de démontrer que la DIC peut être utilisée efficacement pour aider à rendre robuste l’analyse vibratoire. Une telle méthode peut se révéler particulièrement utile pour l’analyse vibratoire dans des situations où les mesures de contact direct sont difficiles à réaliser. Cette approche ouvre des perspectives pour les ingénieurs, en leur offrant un outil puissant pour valider et affiner les modèles de simulation.
Les perspectives futures de ce travail, outre l’application à des cas réels, sont l’application de cette méthode à un comportement vibratoire réalisé par simulation numérique sous chargement, et le couplage des données de DIC avec des données d’accéléromètres pour compléter l’analyse.
