- Par Florent Mathieu, Président et co-fondateur d’EikoSim
Pourquoi une méthode « globale » ?
La corrélation d’images numériques consiste à effectuer une mesure de champ de déplacements entre une configuration de référence et une configuration déformée. Deux grandes familles existent pour faire cette mesure :
- les méthodes « locales » (ou subset-based) répètent une action de recherche pour une série d’imagettes (subsets) positionnées sur une grille dans l’image.
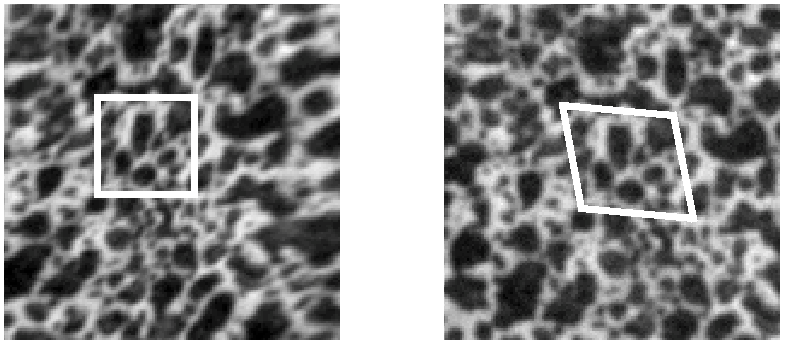
- les méthodes globales reposent sur l’idée que l’introduction d’informations connues (en l’occurrence la continuité du champ de déplacement) dans la formulation du problème doit permettre de réduire les incertitudes de mesure par la diminution du nombre d’inconnues. Cette base peut être choisie comme étant un maillage éléments finis et ses fonctions de forme associées à chaque élément (la méthode est alors dite FE-based).
Dans le cas général, le champ de déplacement u(x) peut être décomposé comme une somme de fonctions de forme Nm :
avec vα m sont les degrés de liberté inconnues du problème, et eα est un vecteur caractéristique de l’élément considéré. C’est la raison pour laquelle on les appelle les méthodes « globales » : tout le champ de déplacement est calculé en même temps, puisque les degrés de liberté sont dépendants les uns des autres. Pour la majorité des cas, où des fonctions de forme éléments finis peuvent être utilisées, les degrés de liberté sont alors simplement les déplacements mesurés aux nœuds.
Trois avantages principaux découlent de l’utilisation de ces techniques :
Une précision de mesure augmentée :
L’algorithme de mesure dispose d’autant d’informations à traiter (les images) mais doit trouver moins d’inconnues, il est donc plus robuste et moins sensible au bruit dans l’image [1].
Les éléments finis assurent la continuité du champ de déplacement :
Cela permet d’éviter des problèmes de discontinuité dans la mesure (du type « élément mal déterminé » localement). On peut également utiliser des méthodes de régularisation « mécanique » [2] et éviter les filtres gaussiens moins adaptés et plus obscurs pour l’utilisateur.
Dans le cas où la continuité du déplacement n’est plus respectée (fissures par exemple), on peut facilement le détecter en observant les résidus de corrélation, qui sont le « reste » de la corrélation entre image de référence et image déformée :
Les résultats sont directement exprimés dans le repère de la simulation :
La principale utilité des éléments finis est la comparaison des mesures à des résultats de simulation. Avec un nuage de points, cette comparaison nécessite des opérations de recalage successives spécifiques à chaque cas, et qui peuvent faire perdre de l’information de mesure (en particulier au moment du passage nuage de points/maillages). Utiliser une méthode globale, c’est parler dans la langue de l’ingénieur simulation, et lui donner directement le résultat de mesure sans avoir besoin de le transformer.
[1] Hild F., Roux S., Comparison of Local and Global Approaches to Digital Image Correlation, Experimental Mechanics 52, pp 1503-1519.
[2] Zvonimir Tomicevic, François Hild, Stéphane Roux, Mechanics-Aided Digital Image Correlation, Journal of Strain Analysis for Engineering Design, SAGE Publications, 2013, 48, pp.330-343
Venez découvrir notre logiciel de mesure par corrélation d’images numériques : EikoTwin DIC !

