- Par Renaud Gras, CTO et co-fondateur d’EikoSim
Recalage et validation des simulations
La simulation joue un rôle accru dans la conception, la qualification et la certification des produits industriels en étant le support des décisions stratégiques de développement. Par conséquent, le rôle des essais a également été modifié, ils constituaient la part essentielle des démonstrations de conformité, mais à présent ils deviennent des référents de validation des simulations numériques [1, 2].
Il est donc de plus en plus nécessaire de recaler et valider les simulations numériques afin qu’elles soient le plus prédictives possible et au plus proche du réel. Ce recalage nécessite d’ajuster le modèle de comportement mécanique de la pièce ou de la structure modélisée en utilisant les données récoltées sur un ou plusieurs essais spécifiés à partir de cette simulation.
Limitations de l’approche traditionnelle
Traditionnellement, lorsque des essais matériaux simples sont effectués, les sollicitations appliquées sont bien maîtrisées, et une instrumentation classique (type jauge de déformation) équipe l’éprouvette. Ces essais standardisés permettent d’obtenir une déformation homogène dans l’échantillon afin d’identifier un paramètre du modèle [3]. Dans ce cadre, la détermination de modèles complexes nécessite beaucoup d’essais. De plus, cette stratégie n’est pas applicable sur les essais de structure pour lesquels la géométrie et les modèles de comportement sont plus complexes.
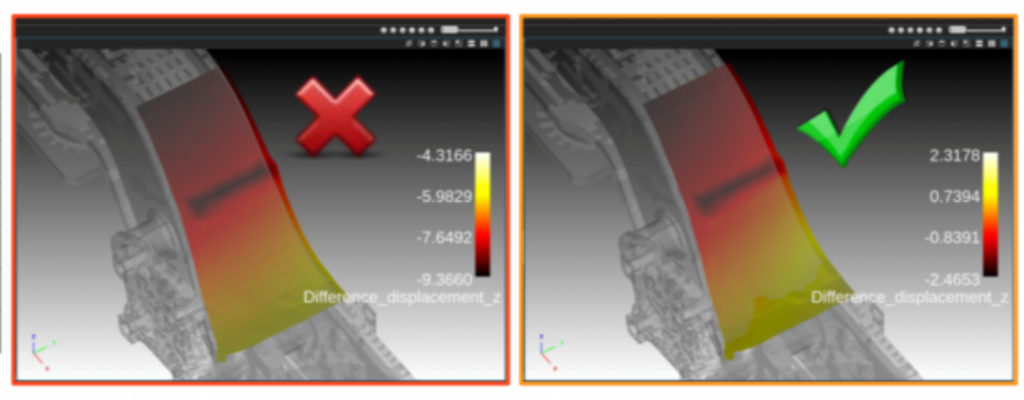
Lors de cette étape de recalage et/ou de validation de la simulation numérique, on observe une perte de continuité des données. En effet, la simulation numérique fournit des résultats (et notamment un champ de déplacement) sur l’ensemble de la pièce. L’information est extrêmement riche et permet de déterminer les zones critiques. Or lors de l’essai, les capteurs utilisés sont le plus souvent ponctuels, qu’il s’agisse de jauges de déformations, de capteurs de déplacement ou encore de lasers. Ces capteurs ne recouvrent pas l’ensemble de la pièce et leurs mesures ne sont pas exprimées dans le référentiel de la simulation, ce qui complique la comparaison essai/calcul. De plus, en cas de désaccord des données expérimentales et simulées, il est souvent extrêmement difficile d’identifier l’origine de cette différence, conséquence de l’aspect ponctuel des mesures. Il est donc possible que la zone critique réelle ne soit pas instrumentée. Cet écart vient-il du comportement, des conditions aux limites, des hypothèses de simplification prises dans le modèle ? Afin de répondre à ces questions, des simulations voire des essais supplémentaires sur prototypes sont nécessaires, ce qui entraîne un dépassement des coûts et des délais du programme de développement.

Le modèle 3D pour assurer la continuité des données
Pour assurer la continuité numérique, il est proposé d’utiliser le modèle 3D depuis la CAO jusqu’à la validation de la simulation. Ce modèle est utilisé :
- pour la spécification de l’essai,
- pour la conception et la réalisation d’essais virtuels dans l’environnement de test incluant les capteurs mis en œuvre sur le prototype,
- pour la mesure sur l’essai réel,
- et enfin pour le recalage et la validation de la simulation numérique.
Pour traiter les deux dernières étapes, l’essai est instrumenté par imagerie et la mesure sur l’essai réel est faite par Corrélation d’Images Numériques [4] en prenant le modèle 3D comme référence.
La mesure est donc réalisée directement dans le référentiel de la simulation numérique, sur le maillage éléments finis. La comparaison entre données d’essais et données de simulation est donc immédiate. De plus en cas de désaccord, la mesure étant riche du fait de l’obtention d’un champ de déplacement, il est possible de déterminer les zones dans lesquelles l’écart est significatif. Ces mesures, exprimées sur le maillage éléments finis, permettent également de réaliser un recalage du modèle de manière automatique par une méthode dite de recalage de modèle éléments finis (FEMU). Cette identification doit être pondérée par l’incertitude de mesure permettant d’obtenir les nouveaux paramètres du modèle ainsi que leurs incertitudes vis-à-vis des données utilisées comme référence. L’apport de techniques de mesure par imagerie permet d’enrichir les données de mesure, et grâce au champ hétérogène mesuré, d’identifier plusieurs paramètres du modèle grâce à un seul essai [5].
Le modèle 3D devient la base d’un jumeau numérique autour duquel les données sont rassemblées.
Vers la bonne prise en compte des différentes sources d’écart
Pour les simulations par élément finis, on retient souvent trois sources d’erreurs : les erreurs de discrétisation, les erreurs de modèle et les erreurs numériques. Les erreurs de discrétisation et les erreurs numériques concernent la vérification des simulations et sont considérés ici comme assez mature pour être contrôlées [6].
Nous considérons donc ici seulement les erreurs de modèle. Celles-ci sont essentiellement dues :
- à la mauvaise application des conditions aux limites, qui diffèrent de ce qui a été appliqué dans les conditions réelles de test,
- au fait que les paramètres du modèle de comportement ne correspondent pas au comportement réel de la pièce.
L’intégration des données d’essai sur le maillage éléments finis utilisé pour la simulation permet de recaler cette simulation par une méthode d’identification. L’article publié récemment par S. Roux et F. Hild propose une méthode optimale d’identification basée sur le choix d’une norme adaptée prenant en compte les incertitudes de mesure [7].
Ces sources d’incertitudes sur les mesures par Corrélation d’Images Numériques sont le bruit dans les images et l’étalonnage. Il est également important de prendre en compte les incertitudes sur les conditions aux limites dues aux jeux dans les assemblages, à l’alignement des vérins ou à la distribution des conditions aux limites appliquées.
Lors du recalage de la simulation, il est primordial de considérer et de séparer les erreurs de modèle de comportement, des erreurs dues aux différences de conditions aux limites entre ce qui a été spécifié dans la simulation et ce qui a réellement été appliqué dans l’essai. Afin de s’affranchir des erreurs dues aux sollicitations mécaniques imposées, la mesure par corrélation d’images numériques faite directement sur le maillage est l’outil adapté. Les conditions aux limites peuvent être mesurées et directement réinjectées dans la simulation numérique. Comme cela a été fait sur le cas d’un châssis de train en collaboration avec ALSTOM et le CETIM.
En considérant que la calibration du système de caméras a été menée correctement, les incertitudes en résultant peuvent être négligées. Il reste donc uniquement les incertitudes de mesure dues au bruit d’acquisition du capteur. Ce bruit, par propagation à travers la méthode de corrélation d’images numériques utilisée, s’exprime sur la mesure de champs de déplacement et, par propagation à travers la méthode d’identification, sur les paramètres identifiés. La bonne prise en compte de cette propagation d’incertitude permet d’obtenir une incertitude sur les paramètres identifiés à partir de la connaissance du bruit d’acquisition des images.
Ayant appliqué les conditions aux limites mesurées dans la simulation et ayant pris en compte les incertitudes de mesure dans la méthode d’identification, on peut alors considérer que les écarts restants entre résultats de mesure et de simulation sont uniquement dus aux paramètres du modèle de comportement.
Pour résumer
Le modèle 3D, pris comme jumeau numérique tout au long du cycle de conception, et associé à des techniques de mesure de champ de déplacement par imagerie, permet donc
- d’assurer la continuité de la chaîne numérique de conception,
- d’agréger les données de simulation et les données d’essai,
- de valider la simulation numérique et en cas de désaccord entre données d’essai et données de calcul de recaler le modèle mécanique implémenté.
La prise en compte des conditions aux limites mesurées par corrélation d’images numériques dans la simulation numérique permet aussi de séparer les erreurs venant de l’application des conditions aux limites dans l’essai et des erreurs de modèle de comportement et par propagation du bruit d’acquisition des images d’obtenir une incertitude sur les paramètres identifiés.
Références
[1] https://www.nafems.org/professional_development/nafems_training/training/verification-validation-des-modeles-et-analyses/
[2] https://www.asme.org/products/codes-standards/v-v-101-2012-illustration-concepts-verification
[3] https://en.wikipedia.org/wiki/Tensile_testing
[4] Dubreuil, L., Dufour, JE., Quinsat, Y. et al. Exp Mech (2016) 56: 1231. https://doi.org/10.1007/s11340-016-0158-x
[5] Jan Neggers, Olivier Allix, François Hild, Stéphane Roux. Big Data in Experimental Mechanics and Model Order Reduction: Today’s Challenges and Tomorrow’s Opportunities. Archives of Computational Methods in Engineering, Springer Verlag, 2018, 25 (1), pp.143-164. https://dx.doi.org/10.1007/s11831-017-9234-3
[6] P. Ladevèze and D. Leguillon. Error estimate procedure in the finite element method and applications. SIAM J. Num. Analysis, 20(3) : 485 – 509, 1983.
[7] Stéphane Roux, François Hild. Optimal procedure for the identication of constitutive parameters from experimentally measured displacement fields. International Journal of Solids and Structures, Elsevier, In press, https://dx.doi.org/10.1016/j.ijsolstr.2018.11.008